书名:怎样解题:数学思维的新方法
英文名:How to Solve It : A New Aspect of Mathematical Method
内容简介
In this best-selling classic, George Polya revealed how the mathematical method of demonstrating a proof or finding an unknown can be of help in attacking any problem that can be “reasoned” out - from building a bridge to winning a game of anagrams.Generations of readers have relished Polya’s deft instructions on stripping away irrelevancies and going straight to the heart of a problem. “How to Solve It” popularized heuristics, the art and science of discovery and invention. It has been in print continuously since 1945 and has been translated into twenty-three different languages. Polya was one of the most influential mathematicians of the twentieth century. He made important contributions to a great variety of mathematical research: from complex analysis to mathematical physics, number theory, probability, geometry, astronomy, and combinatorics. He was also an extraordinary teacher - he taught until he was ninety - and maintained a strong interest in pedagogical matters throughout his long career.In addition to “How to Solve It”, he published a two-volume work on the topic of problem solving, “Mathematics of Plausible Reasoning”, also with Princeton. Polya is one of the most frequently quoted mathematicians, and the following statements from “How to Solve It” make clear why: “My method to overcome a difficulty is to go around it.” “Geometry is the science of correct reasoning on incorrect figures.” “In order to solve this differential equation you look at it till a solution occurs to you.”
本书主打启发式方法( heuristics),本书翻译成探索式方法。
作者简介
乔治·波利亚(George Polya,1887—1985),美国数学家和数学教育家。生于匈牙利布达佩斯。1912年获布达佩斯大学博士学位。1914年至1940年在瑞士苏黎世工业大学任数学助理教授、副教授和教授,1928年后任数学系主任。1940年移居美国,历任布朗大学和斯坦福大学的教授。1976年当选美国科学院院士。还是匈牙利科学院、法兰西科学院、比利时布鲁塞尔哲学科学院和美国艺术和科学学院的院士。其数学研究涉及复变函数、概率论、数论、数学分析、组合数学等众多领域。1937年提出的波利亚计数定理是组合数学的重要工具。长期从事数学教学,对数学思维的一般规律有深入的研究,著有《怎样解题》《数学的发现》《数学与猜想》。
目录
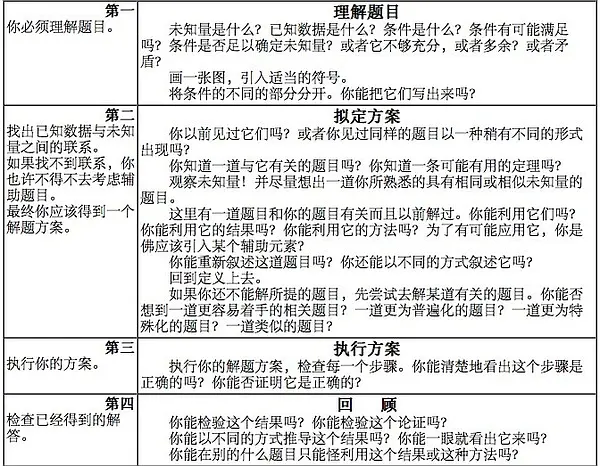
解题四阶段
- 我们必须理解该题目;我们必须清楚地看到所要求的是什么。
- 我们必须了解各个项目是如何相关的,未知量和数据之间有什么关系,已得到解题的思路,拟定一个方案。
- 我们执行我们的方案。
- 我们回顾所完成的解答,检查和讨论它。
第一部分 在教室里
目的
1.帮助学生
2.问题,建议,思维活动
3.普遍性
4.常识
5.教师和学生,模仿和实践
主要部分,主要问题
6.四个阶段
7.理解题目
8.例子
9.拟订方案
10.例子
11.执行方案
12.例子
13.回顾
14.例子
15.不同的方法
16.教师提问的方法
17.好问题与坏问题
更多例子
18.一道作图题
19.一道证明题
20.一道速率题
关键内容:
教师应当把自己放在学生的位置上,他应当看到学生的情况,应当努力去理解学生心里正在想什么,然后提出一个问题或是指出一个步骤而这正事学生自己原本应想到的。
如果同一问题不断地对学生有所帮助,那么他很难会不注意到这一点,而且这将引导他在相似的情况下自己提出这一问题。反复提出这个问题,也许有一次他就会成功地得出正确的概念。由于这一成功,他发现了使用这一问题的正确方法,于是他已经真正地消化这一问题了。
教师提问的方法:建议必须简单和自然,因为不然的话,它们就不可能不露痕迹了。
第二部分 怎样解题
这部分是一段对话,关键内容如下:
- 熟悉题目:尽可能清晰、生动地使整个题目形象化。暂时抛开细节。
- 深入理解题目:当你对题目的叙述已经很清楚,并在脑海里留下深刻的印象,以至于即使你一会儿不去看它也不会担心把它全部忘掉时,就可以开始了。
- 寻求有用的思路
- 执行方案
- 回顾:考虑解答的各个细节,并尽可能使它们显得简单;考察解答中那些比较冗长的部分并尽可能使它们简短些;试着一眼就能看出整个解答。对你的解答中或大或小的各部分进行改进,尝试改进你的整个解答,使它直观,并且尽可能自然地把它纳入你过去所获得知识之中。仔细检查引导你获得解答的方法,注意找出它的要点,并在其他题目中尝试应用它。仔细检查你的结论,并尝试应用于别的题目。
第三部分 探索法小词典
类比:找相似性
辅助元素:引入辅助线等
辅助题目:相关题目
波尔察诺
出色的念头
你能检验这个结果吗?
你能以不同的方式推导这个结果吗?
你能应用这个结果吗?
执行
条件
矛盾
推论
你能从已知数据中得出一些有用的东西吗?
你能重新叙述这道题目吗?
分解和重组
定义
笛卡儿
决心、希望、成功
诊断
你用到所有的已知数据了吗?
你知道一道与它有关的题目吗?
画一张图
检验你的猜想
图形
普遍化
你以前见过它吗?
这里有一道题目和你的题目有关
而且以前解过
探索法
探索式论证
如果你不能解所提的题目
归纳与数学归纳
创造者悖论
条件有可能满足吗?
莱布尼茨
引理
观察未知量
现代探索法
符号
帕普斯
拘泥与变通
实际题目
求解题、证明题
进展与成绩
谜语
归谬法与间接证明
多余
常规题目
发现的规则
格式的规则
教学的规则
将条件的不同部分分开
建立方程
进展的标志,
特殊化
潜意识活动
对称性
新旧术语
量纲检验
未来的数学家
聪明的解题者
聪明的读者
传统的数学教授
变化题目
未知量是什么?
为什么证明?
谚语的智慧
倒着干
关键内容:
- simplex sigillum veri. (拉丁语:简单性是真理的标志)
- 教师们和教科书的作者们不应该忘记一点:聪明的学生和聪明的读者不会满足于只验证推理的各个步骤都是正确的,他们也想知道各个不同步骤的动机和目标。
- 在一步步地检验一个论证时,我们应该避免单纯的重复。首先,单纯的重复容易使人厌烦、缺乏启发性、导致注意力涣散。其次,如果情况和上一次相同,我们很可能在犯过错误的地方再错一次。如果我们觉得有必要将整个论证一步一步地再过一遍的话,我们至少应该改变一下这些步骤的次序或组合,来引入一些变化。
- 如果一个学生从来没有机会解答一道由他自己创造的题目,他的数学经验就是不完整的。
- 欧几里得的论证方式,即严格地从已知数据进展到未知量,从题设进展到结论的方法,用来详细地检查论证过程是很好的,而用来使我们理解论证的主要思路则还远远不够好。
- 直观的洞察和形式上的证明是获得真理的两种不同的方式,这可以与通过视觉和触觉这两种不同的感官来感知一种事物想比拟。
- 如果你深入细节中去,你就可能会在细节中迷失自我。过多过细的枝节对思维是一种负担。它们会阻碍你对要点投入足够的注意力,甚至会使你全然看不到要点。
- 如果我们想研究一些更深入的细节,我们应该做什么?在通常的情况下,可取的做法是,研究每个数据本身,将条件的不同部分分开,并研究每一个部分本身。
- 教学生解题也是一种意志的教育。学生要解决对他来说并不容易的题目,他将要学会面对失败起而不舍,重视小的进步,静候实质性的念头,当这一念头出现后全力以赴。如果学生在学校中没有机会使自己体会到这种为解题奋斗而带来的各种情绪变化,他的数学教育就在最重要的一点上失败了。
- 有的学生完全没有计划和总体思想,就急于计算和作图;另一些学生则傻傻地干等着某个念头出现,而不会做任何事来加速它的到来。
- 不要让你的怀疑、猜想或臆测不加检验地膨胀,直至它变得根深蒂固。无论如何,从理论上说,最好的念头会因不加鉴别而受损,却会因严格的检验而茁壮。
- 越是宏大的计划,越有机会获得成功。较全面的定理可能更容易证明;较普遍的题目可能更容易解答。
- 说和想是紧密联系的,文字的使用有助于思维。
- 相同的一些对象充满了分析和综合过程。它们在分析中锻炼人的思维,在综合中锻炼人的体力。分析存在于思维之中,综合存在行动之中。还有另外一个不同的之处在于:它们的次序恰好相反。
- 为了捷达一道题目的一些只是,此外还还必须在我们已经存在的,但原本潜伏着的知识中挑选和收集相关的内容。从记忆中萃取相关元素可以称为动员。然而,要解答一道题目,仅仅回忆起一些孤立的事实是不够的,我们必须把它们组合起来,而且它们的组合必须能很好地适用于我们手头地题目。这种改编和结合地活动可以称之为组织。事实上,动员和组织不可能真正分开。
- 发现的规则。第一条发现的规则是要有智力和好运。第二条发现的规则是安稳地做下来等待,直到你产生一个出色的念头。
- 格式的规则。第一条格式的规则是要有话可讲。第二条格式的规则是,当你碰巧有两件事要讲时,你要控制好自己,先讲第一件,再讲第二件,不要同时讲两件事。
- 教学的规则。第一条教学的规则时要知道你应该教什么。第二条教学的规则是要懂得比你应该教的东西多一点。
- 在将条件作为一个整体理解了以后,我们将它的不同部分分开,并分别考虑它的每一个部分。
- 因而,清楚地理解未知量地性质就意味着进展;清晰地处置不同数据从而使我们能轻易地想起其中地任何一个,也意味着进展。将条件作为一个整体来进行生动具体地想象可能意味着一个重要的进展,而把条件分成几个适当的部分也许是向前迈出了重要的一步。当我们找到了一个容易想象的图像,或者是一个容易记忆的符号,我们就有理由相信我们已经取得了某个进展。回忆一道与我们的题目有关并且以前解过的题目,也许是朝正确方向迈出了决定性一步。
- 始终跟着你的灵感走——但保持一点怀疑。
- 探索式的:如果A则有B。因为B为真,所以A更可信。
- 证明性的: 如果A则有B。因为B为假,所以A为假。
- 对于探索式的方法,首先,它没有严格证明的确定性;其次,它们本质上对于获取新知识式很有用的,对于任何非纯数学或逻辑的知识,以及对于涉及物质世界的任何知识甚至都是不可或缺的。
- 这种偶发事件给人的印象式潜意识活动。事实是,一道题目在经过一段时间的搁置后,可能回重新回到意识中来,而且基本上一清二楚了,比我们把它们抛在脑后时与解答要接近得多。谁使它清楚了,谁使它更接近答案了?明显的,这就是你自己,你一直在潜意识中活动。除此以外,很难给出其他什么答案,虽然心理学家们已经发现了另一种答案的开始部分,也许有朝一日它会更令人满意。
- 不管潜意识的理论有没有价值,确定无疑的是,存在一个限度,超出了这个限度我们就不能迫使意识作出反应。
- 不过将我们希望稍后回头再做的题目没有取得任何成就的情况下就搁置一边则是不可取的;再停止工作以前题目至少应该已经解决了一点,问题的某个方面应有所阐明。
- 只有那些我们热切地希望解答地题目,或是我们曾经很紧张地解答过地题目,回头再来做时才会有所进展;看来要使潜意识活动继续,主观意识地努力和紧张也是必不可的。
- 如果一道题目具有某些方面的对称性,我们常常能得益于注意到它可以互换的部分,而且常常值得我们用同样的方式来处理那些起相同作用的部分。
- 未来的数学家应该是一个聪明的解题者,但仅仅做一个聪明的解题者是不够的。在适当的时候,它应该去解答重大的数学问题,而且首先他应该搞清楚他的天资特别适合于哪些类型的题目。
- 对他来说,工作中最重要的那部分就是回去再看一下完整的解答。
- 和其他所有人一样,未来的数学家通过模仿和练习来学习。他应该注意寻找正确的典范来模仿;他应该觉察到一个能激励人心的教师;他应该和一位能干的朋友竞赛。然后,可能最重要的是,他不仅应该阅读通用的教材,还应阅读优秀作者的作品,直到他找到一个作者,其方式是他天生倾向于模仿的。他应该欣赏和寻求在他看来简单的或有启发性的或美的东西。他应该解题,选择适合他思路的那些题目,思考它们的解答,并创造新的题目。他应该通过这些方法及所有其他方法来努力作出他的一个重大发现:他应该发现自己的好恶、趣味以及自己的思路。
- 聪明的解题者首先要做的是尽可能充分、清楚地理解题目。然而光有理解是不够的;他必须全神贯注于题目,他必须热切地期望获得解答。如果他不能真正唤起解题地欲望,还不如置之不理。获得真正成功地公开秘密就是要全身心地投入到题目中去。
- 一个聪明地数学书读者有两种愿望:首先,看到论证地当前一步是正确的。其次,看到当前一步的目的。
- 解题的成功决定于选择的正确的角度,决定于从容易接近的一侧来攻克要塞。为了找出哪一个角度是正确的,哪一侧是容易接近的,我们要尝试各种侧面和角度,我们要变化题目。
- 我们不能指望没有极度的专心就能解答什么有价值的题目。但是如果非常专心地集中注意力于某一点上,我们很容易就会感到疲劳了。为了保持我们的注意力活跃,注意力指向的对象必须不断地变化。
- 我们常常必须对题目作不同的修改。我们必须一次又一次地变化、重述、变换,直到最终成功地找到一些有用的东西。我们可以在失败中学习,在一次不成功的尝试中也许会有某个好的想法,而且我们通过修改一次不成功的尝试也许可以得到一个更为成功的尝试。
- 如果一本教科书的作者含含糊糊地提出一个不完全证明,其中可以明显看出他对于证明地完全性是该羞愧还是该自负游移不定,那将是痛苦的。但是当不完全证明在适当的地方得体地提出时,他也会有用。它们的目的不是要去代替完全证明(这是它们绝对不可能办到的),而是要使问题的陈述又趣味性和连贯性。
- 不完全证明可以作为一种助记手段。
- 将关于制定计划、寻找方法和选择行动路线的谚语(简单说,就是关于解题的谚语)进行收集和归类会是一项有意思的任务。
- 智者从目标着手,愚者在起点止步。
- 钓鱼不在于钓而在于鱼。
- 多思出上策。
- 当你找到第一个蘑菇或作出第一个发现后,再四处看看;它们总是成群生长。
第四部分 题目、提示、解答
题目
提示
解答
注释