概论
前言
《从一到无穷大》第一章中关于大数字的部分非常有趣。书中提到“墙上的板子似乎连‘十万’这个数字都难以写下”,这一细节生动地展示了蛮夷戎狄面对巨大数字时的局限感。
西洋人的”古代“历史书中既没有时间(比如希罗多德的《历史》),也没有标志性的罗马大数字。这让我不禁怀疑古罗马真的有几千万人口这一说法是否确凿,是否仅仅是借鉴了类似大漢的记录才得出这些数据。通过观察我发现,后世对苏格拉底的描述渐渐带上了更多孔子的影子,古罗马帝国繁荣的描述也似乎包含了许多两漢时期的影子。
总体来说,这本书内容丰富,视角独特,非常值得一读。
书籍简介
作者: 【美】 乔治·伽莫夫
出版社: 天津人民出版社
出品方: 果麦文化
原作名: One Two Three… Infinity: Facts and Speculations of Science
译者: 阳曦
出版年: 2019-9
页数: 424
定价: 58.00元
装帧: 平装
ISBN: 9787201151304
内容简介
从一粒原子,到无穷宇宙,一本书汇集人类认识世界、探索宇宙的方方面面:数论、世界线、相对论、量子力学、核物理、遗传学……
这本书将会回答你如下问题:无穷大究竟有多大?空间有里外之分吗?为什么三维世界里的人无法想象四维空间?相对论是怎么“相对”的?我们怎么才能看到原子的尺寸?核反应时究竟在发生什么?生物与非生物的界限在哪里?
一,二,三……快进入无穷大的科学世界吧!
作者简介
乔治·伽莫夫,著名物理学家、天文学家,“大爆炸”理论推动者,提出了生物学的“遗传密码”理论,以及放射性量子论和原子核的“液滴”模型。顶级科普作家,一生共撰写25部科普作品,其中以《从一到无穷大》最为著名与经典,风靡全球数十年,被译成十几种语言畅销各国,启迪了无数热爱科学的年轻人走上科学的道路。因为他在科普方面的巨大成就,1956年联合国教科文组织授予他卡林伽科普奖
阳曦,专注科普作品翻译与科幻文学创作。在《科幻世界》等杂志发表多部原创作品,《环球科学》等杂志长期合作译者。科技部“全国优秀科技作品奖”得主,已出版译作《赶往火星》《消失的调羹》《他们应当行走》等。
正文摘录
前言
……譬如原子、恒星、星云、熵和基因;譬如人能不能弯曲空间,火箭为什么会缩短。是的,在这本书里,我们将讨论以上所有问题,以及其他很多同样有趣的东西。
我之所以想写这样一本书,是为了尽可能地搜集现代科学中最有趣的事实和理论,从微观到宏观,为读者描绘一幅全面的宇宙图景,让他们知道如今科学家眼里的世界是什么样子。为了实现这个宏伟的计划,我不打算完整地介绍每一套理论,否则这本书势必变成多卷本的百科全书;不过与此同时,我挑选主题的标准是尽量覆盖基础科学知识的方方面面,不留下任何死角。
筛选主题的时候,我依据的主要是它们的重要性和有趣程度,而不是专挑简单有用的东西来说,这样的做法势必造成表述上的不均衡。本书的部分章节非常简单,就连孩童都能轻松看懂;但也有一些章节需要读者略微集中精力、做一点儿研究才能完全理解。不过普通读者在阅读本书时应该不会遇到太大的困难,至少我希望如此。
你可能会注意到,本书后半部分讨论“宏观宇宙”的部分比前面讨论“微观世界”的章节简短得多。这主要是因为我在《太阳的诞生和死亡》和《地球小传》 两本书中已经深入讨论了关于宏观宇宙的很多问题,现在再多费唇舌无疑会显得冗长而重复。因此,在这本书里,我只是大体描述了关于行星、恒星和星云的物理学常识以及主宰它们的规律,只有在介绍近年来科学进展带来的最新发现时,我才会多花费一些笔墨。根据这一原则,我重点介绍了由所谓的“中微子”(它是物理学家所知的最小粒子)引发的大规模恒星爆炸,人们将它命名为“超新星”,以及新的行星理论:这套理论重新构建了康德和拉普拉斯几乎已经被人遗忘的古老观点,也推翻了目前学界广泛认可的看法,即行星起源于太阳和其他恒星的碰撞。
我衷心感谢许许多多的艺术家和插图画师,他们的作品经过拓扑变换(见第二卷第三章),为本书的很多插图提供了基础的素材。我最想感谢的是一位年轻的朋友——玛丽娜·冯·诺依曼。玛丽娜宣称自己什么事都比她那位著名的父亲懂得多,当然,数学除外;她表示,对于这门学科,她所知的不过和父亲相仿而已。读了本书部分章节的草稿以后,玛丽娜告诉我说,很多东西她都看不懂,所以我只好承认,本书不适合儿童阅读,这和我当初想的不太一样。
G.伽莫夫 1946年12月1日
1961年版前言
所有关于科学的书籍在付梓几年以后都很容易变得过时,如果你介绍的是那些正在飞速发展的科学领域,那更是难逃厄运。我这本《从一到无穷大》虽然已经出版了十三年,却幸运地躲过了这个魔咒。在本书问世前不久,科学界取得了一系列重要成果,我在写作中已经纳入了这部分内容,所以时至今日,我只需要做一点修改和增补就能追上最新的发现。
这些重要成果包括原子能的成功释放,它的具体表现形式是基于热核反应的氢弹爆炸,科学家的下一个目标是实现热核过程的可控能量释放。虽然他们目前尚未取得太大的突破,但研究工作仍在稳步推进。在本书第一版第十一章中,我已经介绍了热核聚变的原理和它在天体物理学领域的应用。要进一步囊括最新的进展,我只需要在第七章末尾增加一些新的内容。
除此以外还有一些变化:我们估算的宇宙年龄从原来的20亿到30亿年增长到了现在的50亿年以上 ,加州帕洛马山之巅新竖起的200英寸海尔望远镜的最新观测结果也帮助我们完成了天文距离尺度的修订。
生化领域的新进展迫使我修改了图101及其说明文字,并在第九章末尾增加了一些关于简单生命体合成反应的新内容。在本书的第一版中,我曾写道:“是的,生命和非生命物质之间当然有一个过渡的步骤,有朝一日——或许就在不久的将来——等到某位天才生化学家终于用普通的化学元素合成了病毒分子,他就可以骄傲地宣布:‘我刚刚赋予了死物质生命的气息!’”呃,几年前,加州的科学家真的完成了——或者说几乎完成了——这一壮举。在第九章的末尾,诸位读者可以看到关于这项工作的简单介绍。
最后还有一个变化:本书第一版题词写着“献给我的儿子伊戈尔,他是个想当牛仔的小伙子”。很多读者写信来问,伊戈尔后来有没有实现理想。我只能回答,没有;明年夏天他即将毕业,学的是生物,现在他打算从事基因方面的工作。
G.伽莫夫 科罗拉多大学 1960年11月
第一卷 数字游戏
第一章 大数字
1 你能数到几?
与此同时,恺撒办公室里的书记员会这样写:
MMMMMMMMDCCXXXII
后面这组符号你肯定觉得很眼熟,因为直到今天,我们偶尔还会使用罗马数字——比如说,用于标记书中的章目,或者在装饰华美的纪念碑上记录某个历史事件的时间。由于古人需要记录的数字最大也不过是几千而已,所以他们根本没有千位数以上的数字符号;哪怕是最精于算术的罗马人,如果你要求他写个“一百万”,他也只能束手无策;如果你继续坚持,那他只能连续写一千个“M”,这够他辛苦好几个小时(见图1)。

一位打扮类似奥古斯都·恺撒的古罗马男子试图用罗马数字写出“一百万”。墙上这块板子看起来连“十万”都不太写得下。
对古人来说,那些特别大的数字都是“不可数”的,譬如天空中有多少星星,海里有多少条鱼,或者海滩上有多少粒沙子;于是他们只好像数不到“5”的霍屯督人一样,简单地概括说,“很多”!
……
事实上,这样一台自动印刷机必将印出自人类学会写字以来所有人写过的所有东西:每一行散文和诗歌、每张报纸上的每一篇社论和广告、每一部沉闷的科学论著、每一封情书、每一张留给送奶工的纸条……
除此以外,这台机器还将印出未来的人们将要写下的所有东西。我们将在圆盘印出的纸张上找到30世纪的诗歌、未来的科学发现、第500届美国国会的演讲稿,以及2344年的行星际交通事故报告。我们将看到尚未被人类之手写出的无数短篇故事和长篇小说,要是出版商的地下室里有这么一台机器,那他们只需要从大量垃圾里挑出这些佳作进行编辑就好——反正他们现在也是这么干的。
2 无穷大有多大
上一节中我们讨论了数字,其中很多数字相当大。尽管这些数字界的巨无霸(例如西萨·本要求的麦粒数量)大得超乎想象,但它们依然是有限的,只要有足够的时间,你总能将它数到最后一位。
但世界上还有一些真正“无穷大”的数字,无论你花多少时间都写不完。比如说,“所有数字的数量”显然无穷大,同样的还有“一条线上所有几何点的数量”。除了“无穷大”以外,你还能用什么办法来描述这样的数字?或者说,我们能不能比较两个不同的“无穷数”,看看它们谁“更大”?
“所有数字的数量和一条线上所有点的数量,这两个数到底哪个大?”我们能这样问吗?著名数学家格奥尔格·康托尔(Georg Cantor)头一次认真审视了这些被视作异想天开的问题,他是当之无愧的“无穷数学”奠基者。
……
这就是康托尔提出的比较两个“无穷数”的方法:我们可以对两组无穷数进行配对,每个集合里的一个元素分别对应另一个集合里的一个元素,如果最后它们正好一一对应,任何一个集合都没有多余的元素,那么这两个数的大小相等;但是,如果两组无穷数无法一一对应,某个集合中存在无法配对的剩余元素,那么我们可以说,这个集合的无穷数更大,或者更强。
这显然是最合理的办法。事实上,要比较无穷大的数字,我们也只有这个办法;但是,如果你真的打算采用这种办法,那你得做好大吃一惊的准备。比如说,奇数的数量和偶数的数量都是无穷大,我们先来比较一下这两个无穷数。当然,出于直觉,你肯定认为这两个数相等,它们也完全符合我们刚才描述的规律,奇数和偶数可以列成一对一的组合:
在这张表格中,每个偶数都有一个对应的奇数,反之亦然;因此,奇数的数量和偶数的数量是两个相等的无穷数。看起来真的非常简单自然!
不过,请稍等一下。下面两个数你觉得哪个更大:所有数字(包括奇数和偶数)的数量和偶数的数量?你当然会说,肯定是所有数字的数量更大,因为除了偶数以外,它还包含了奇数。不过这只是你的直觉,要找到准确答案,你得严格按照我们上面描述的方法来比较这两个无穷数。这样一来,你会惊讶地发现,你的直觉错了。事实上,所有数字的集合和只有偶数的集合也能做成一张一一对应的表格:
根据无穷数的比较规则,我们只能说,偶数的数量和所有数的数量是两个相等的无穷数。这听起来当然很矛盾,因为偶数只是所有数字的一部分,但我们必须记住,这里讨论的是无穷数,所以我们只能做好准备,直面它们的古怪特性。
事实上,在无穷数的世界里,部分可能等于整体!这方面最好的例子大概是德国数学家大卫·希尔伯特(David Hilbert)讲的一个故事。据说希尔伯特曾在开讲座的时候这样描述无穷数的矛盾特性:
“我们不妨想象一家旅馆,它的房间数量是有限的。现在所有房间都住满了,一位新来的客人想要一个房间,‘对不起,’店主回答,‘但我们已经客满了。’接下来,我们再想象一家拥有无穷多个房间的旅馆,所有房间同样住满了。这家旅馆也来了一位想住店的新客人。
“‘当然可以!’店主热情地喊道。于是他将原来住在N1号房的客人挪到N2号房,N2号房的客人挪到N3,N3的挪到N4,以此类推……最后新客人住进了刚刚腾出来的N1号客房。
“现在我们继续想象,一家旅馆拥有无穷多个房间,现在来了无穷多个想住店的新客人。
“‘没问题,先生们,’店主回答,‘稍等一下。’
“他让N1号房的客人挪到N2号房,N2的挪到N4,N3的挪到N6,以此类推……
“现在所有奇数号的房间都空了出来,无穷多位客人轻轻松松就安置了下来。”
呃,哪怕在战时的华盛顿,要想象希尔伯特描述的这种情况也并不容易,但这个故事抓住了问题的重点:无穷大的数字的确拥有一些不同于普通数字的古怪特性。
根据康托尔的“无穷数比较法则”,我们现在还能证明分数(例如3/7或者735/8)的数量等于整数的数量。事实上,我们可以根据如下规则将所有分数排成一行:先写下分子与分母之和等于2的分数,这样的分数只有一个:1/1;然后写下分子分母之和等于3的分数:2/1和1/2;接下来是分子分母和为4的:3/1,2/2,1/3。以此类推,最终我们将得到一个包含了所有分数的无限长的数列(见图5)。现在,我们在这个数列上方写下整数数列,让这个数列中的每个项和分数数列一一对应。最后你会发现,分数的数量和整数的数量相等!
……
因此,一条线上的点和整数之间无法建立一一对应的关系,这意味着一条线上点的数量大于,或者说强于所有整数或分数的数量。
我们刚才讨论的点来自一条“1英寸长”的线,不过现在,根据 “无穷数学”,我们可以轻松证明,同样的结论适用于任意长度的线。事实上,无论线的长度是1英寸、1英尺还是1英里,它拥有的点的数量完全相等。为了证明这一点,我们只需要看看图6,这幅示意图比较了两条长度不同的线段AB和AC拥有的点的数量。为了在两条线段之间建立一一对应的关系,我们从其中一条线段上的每一个点出发,画了一组无穷多条的平行线,每条平行线与两条线段的交点分别是D和D1,E和E1,F和F1,以此类推。AB上的每一个点在AC上都有对应的一点,反之亦然。因此,根据无穷数的比较法则,两条线段拥有的点的数量完全相等。
遵循同样的原则,我们还有一个惊人的发现:一个平面上的所有点的数量等于一条线上的所有点的数量。
线段AB上每一个点的位置都能用一个数字来描述,譬如0.75120386……我们可以取小数点后的奇数位和偶数位,分别组成两个数字,即0.7108……和0.5236……
现在用这两个数分别代表正方形内某个点的横坐标和纵坐标,于是我们得到了平面内的一个“对应点”。反之,如果平面内某个点的横坐标和纵坐标分别是0.4835……和0.9907……,那么将这两个数字融合在一起,我们同样可以得到线段AB上的对应点:0.49893057……
显然,通过这样的方法,我们在这两组点之间建立了一一对应的关系。线段上的每一个点在平面内都有一个对应点,反之亦然,双方都不会落下哪怕一个点。因此,按照康托尔的标准,平面内所有点的数量等于线上所有点的数量。
通过类似的方式,我们也很容易证明,立方体内所有点的数量等于平面或线段内所有点的数量。要完成这个任务,我们只需要把最初的那个小数分成三个部分,再用这三个点作为坐标来寻找立方体内的“对应点”。进一步说,既然两条任意长度的线段拥有的点数量相等,那么任意正方形和立方体(无论大小)拥有的点数量也完全相等。
虽然几何点的数量大于整数和分数的数量,但它还不是数学家所知的最大的数。事实上,我们发现,曲线的种类(包括那些形状最不同寻常的曲线)大于几何点的数量,因此我们必须用无穷数列的第三个数来描述它。
“无穷数学”的奠基者格奥尔格·康托尔提出,我们可以用希伯来字母ℵ(aleph)来描述无穷大的数字,字母右下方的角标代表该数字在无穷数列中的位置。于是我们得到了这样一个数列(包括无穷数!):
1,2,3,4,5,……ℵ₀,ℵ₁,ℵ₂,ℵ₃……
现在我们可以说,“一条线上有ℵ₁个点”,或者“曲线共有ℵ₂种”,就像平时我们说“世界分为7个部分”或者“一副牌有52张”一样。(见图8)
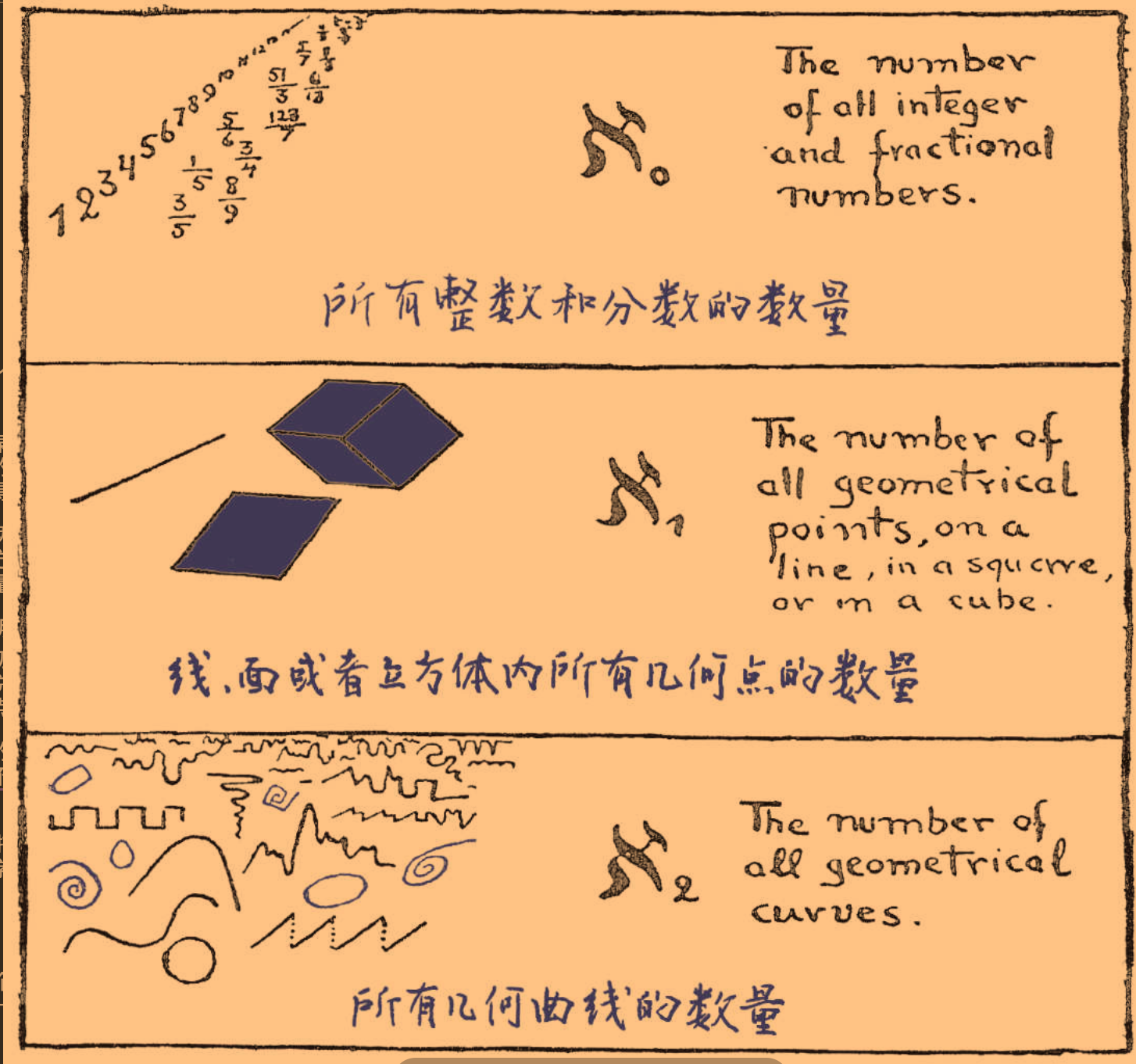
前三个无穷数
在无穷数的话题结束之前,我们必须指出,无穷数的增长速度极快,很快就会超越任何我们能想到的集合。我们知道,ℵ₀代表所有整数的数量,ℵ₁代表所有几何点的数量,ℵ₂代表曲线的所有种类,但截至目前,还没有任何人能找到可以记作ℵ₃的集合。看来前三个无穷数足以穷尽我们能想到的一切事物,所以我们现在的处境和那位有很多儿子却只能数到3的霍屯督老朋友正好相反!
第二章 自然数字和人造数字
1 最纯粹的数学
数学通常被人们,尤其是数学家视为科学界的皇后,作为皇后,它自然不愿意和其他任何学科产生暧昧的关系。因此,在某次“理论数学与应用数学联合会议”上,有人请大卫·希尔伯特作一次公开演讲,希望借此弥合两派数学家之间的隔阂。希尔伯特是这样开场的:
“我们常听别人说,理论数学和应用数学互为寇仇。但实情并非如此。无论是过去、现在还是未来,理论数学和应用数学从来就不是寇仇,事实上,它们也不可能成为寇仇,因为二者之间毫无相似之处。”
不过,虽然数学情愿保持超然的地位,尽量远离其他学科,但反过来说,其他学科(尤其是物理)却很喜欢数学,它们总是竭尽所能地想跟数学“打成一片”。事实上,时至今日,理论数学几乎所有分支都已经成为科学家解释物理世界的工具,其中包括那些曾经被人们认为纯粹得没有任何实用价值的理论,例如群论、非交换代数和非欧几何。
不过,哪怕是在今天,数学领域内仍有一套庞大的体系一直坚守着“无用”的高贵地位,它唯一的作用就是帮助人们锻炼智力,这样的超然绝对配得上“纯粹之王”的桂冠。这套体系就是所谓的“数论”(这里的“数”指的是整数),它是最古老、最复杂的理论数学思想之一。
奇怪的是,尽管数论的确是最纯粹的数学,但从某个角度来说,它又是一门基于经验甚至实验的科学。事实上,数论的绝大多数命题来自实践——人们尝试用数字去做各种事情,然后得到一些结果,由此形成理论。这样的过程和物理学别无二致,只不过物理学家尝试的对象是现实中的物体而非理论化的数字。数论和物理学还有一个相似之处:它们的某些命题得到了“数学上”的证明,但另一些命题仍停留在经验主义的阶段,等待着最杰出的数学家去证明。
2 神秘的$\sqrt{-1}$
利用−1的平方根这个虚数,人们还找到了另一座惊人的宝藏:我们习以为常的三维空间竟能和时间结合起来,形成一个符合四维几何学的统一坐标系。不过这方面的发现,我们可以留到后面讨论阿尔伯特·爱因斯坦和相对论的章节再讲。
第二卷 空间、时间和爱因斯坦
第三章 宇宙的奇异特性
1 维度和坐标
对于习惯了三维空间的我们来说,要想象大于三个维度的超空间(不过我们很快就将看到,这样的空间的确存在)无疑是件难事;但反过来说,想象小于三个维度的低维空间就简单多了。平面,球面,或者其他任意什么面,这都是二维空间,因为我们只需要两个数就能表达这个面上任意一点的位置。以此类推,线(无论直线还是曲线)是一维空间,在这样的空间中描述位置只需要一个数。我们还可以说,点是零维空间,因为一个点内的任何位置都没有区别。但谁也不会对点有多大的兴趣吧!
作为三维生物,我们很容易理解线和面的几何性质,因为你可以“从外面”观察;不过要理解我们身处其中的三维空间,那就难得多了。所以你可以毫无障碍地理解曲线和曲面,但要说三维空间也可以是弯曲的,你大概就会一脸茫然。
不过只要稍加练习,深入理解“弯曲”这个词的确切意义,你会发现,“弯曲的三维空间”这个概念其实相当简单;到了下一章的末尾,(我们希望!)你甚至可以轻松自如地讨论另一个乍看之下十分可怕的概念:弯曲的四维空间。
不过在此之前,我们不妨做做思维体操,学习一些关于三维空间、二维面和一维线的特性。
2 不用度量的几何学
你大概还记得课本上的几何学,根据你的记忆,这是一门度量空间的科学,它的主要内容是一大堆定理,分别描述各种各样的距离和角度的数值关系(比如说著名的毕达哥拉斯定理,它描述的就是直角三角形边长的数值关系);但事实上,要研究空间最基本的特性,很多时候你根本不必测量任何长度和角度。几何学的这个分支被称为位相几何学(analysis situs)或者拓扑学(topology),它是数学中最困难也最刺激的一个部分。
3 翻转空间
前面我们讨论的拓扑学特性都基于各种面,也就是只有两个维度的亚空间;不过显然,对于所有人生活于其中的三维空间,我们也可以提出类似的问题。如此一来,三维空间中的地图上色问题可以这样表述:我们需要用材质和形状各不相同的原料块搭建一个“空间马赛克”,任意两个材质相同的原料块都不得有共同的接触面,那么我们至少需要多少种材质?
讨论上色问题的时候,对应球面或环面的三维空间应该是什么样的呢?我们能不能设想一些特殊的三维空间,它与正常空间的关系正好类似球面或环面与正常平面的关系?乍看之下,这个问题似乎很不合理。事实上,虽然我们能够轻松想出各种形状的面,但与此同时,我们却总觉得三维空间只有一种,即我们生活于其中的熟悉的物理空间。但这样的观念富有欺骗性,非常危险。只要发挥一点儿想象力,其实我们能够想出一些和教科书上介绍的欧氏空间很不一样的三维空间。
想象这类空间的困难主要在于,作为三维生物,我们只能“从里面”观察空间,而不能像研究特殊的面那样“从外面”观察。不过借助一些思维体操,我们可以不太困难地征服这些特殊空间。

莫比乌斯面和克莱因瓶
第四章 四维世界
1 时间是第四个维度
以此类推,我们还可以回答关于四维物体特性的很多问题。只是无论怎么尝试,我们可能都无法“想象”,我们这个物理空间中还有第四个独立的维度。
但只要再想想,你会发现第四维其实并不神秘。事实上,有一个词我们大部分人每天都会用到,它可以被视为,或者说实际上就是物理世界中的第四个维度,这个词就是“时间”。在我们描述周围发生的事件时,时间常常是一个和空间并列的度量。当我们谈到宇宙中发生了什么,无论是你在街上意外邂逅了一位老朋友,还是一颗遥远的恒星发生了爆炸,一般情况下,我们不光会提到事件发生的位置,还会陈述它发生的时间。通过这种方式,我们为三维空间中的事件引入了第四个维度:日期。
进一步思考这个问题,你也很容易发现,每个物理物体都有四个维度,其中三个是空间维度,还有一个是时间维度。你住的房子在长度、宽度、高度和时间这四个维度上延展,它在时间维度上的跨度始于建成之日,终于毁灭那一天——无论是烧毁、拆毁还是因年久失修而倒塌。
确切地说,时间这个维度和空间的三个维度不太一样。时间的跨度(间隔)由钟表来度量,秒针嘀嗒嘀嗒,整点叮咚报时;而测量空间距离的工具是尺子。你可以用同一把尺子测量长度、宽度和高度,但却不能把它变成钟来测量时间。除此以外,你可以在空间中向前、向右或者向上移动,然后再返回原地,但时间一路向前,从不回头,你只能被动地从过去来到现在,再去往未来。尽管时间的维度和空间的三维有这么多的不同之处,但我们依然可以将时间当成第四个维度,用它来描述这个世界上的物理事件,只是不要忘了,时间和空间的确不太一样。
2 时空等价
如果将时间视为和空间的三个维度大致等价的第四个维度,我们势必面临一个相当困难的问题。测量长度、宽度和高度的时候,我们可以采用同样的单位,譬如说1英寸,或者1英尺。但时间间隔无法用英尺或英寸来衡量,我们必须采用另一套完全不同的单位,例如分钟或小时。那么这两套单位该如何放到一起比较呢?若要想象一个边长为1英尺的四维立方体,它在时间维度上的跨度应该是多少,才能使得四维等长?1秒、1小时还是1个月?1小时应该比1英尺长还是短?
乍看之下,这个问题似乎毫无意义,但要是深入思考一下,你会发现,或许我们可以找到一种合理的方式,将长度和时间跨度放到一起来比较。你常常会听到这样的说法,某人住的地方“离市中心20分钟车程”,或者某个地方“坐火车只要5个小时”就能到。这里我们用搭乘特定交通工具跨越某段距离所需的时间来衡量长度。
因此,如果能找到一种公认的标准速度,我们就能用长度单位来描述时间跨度,反之亦然。当然,作为空间和时间的基本换算因子,我们选定的标准速度必须是一个基本的通用常数,不受人类主观因素或物理环境的影响。在物理学领域里,只有一种速度具备这样的通用特性,那就是真空光速。虽然人们常常叫它“光速”,但更科学的描述应该是“物理相互作用的传播速度”。因为在真空中,物体之间的任何一种力(无论是电磁力还是引力)都以同样的速度传播。此外,正如我们即将看到的,光速代表着宇宙中的速度上限,任何物体在空间中的运动速度都不可能超过光速。
最早尝试测量光速的先驱是17世纪的著名意大利科学家伽利略·伽利莱(Galileo Galilei)。一个漆黑的夜晚,伽利略带着助手来到佛罗伦萨附近的旷野里,他们两个人分别提着一个带有机械遮光板的灯笼,站在相距几英里的两个点上。在某个约定的时刻,伽利略打开遮光板,灯笼的光立即射向助手的方向(图31A),助手看到伽利略发出的灯光信号就会立即打开自己这边的遮光板。光从伽利略的位置传播到助手的位置,然后再传回来,这个过程需要一定的时间,所以按照他们的预想,从伽利略打开遮光板到他看到对面的灯光之间应该会有一个延迟。他们的确观察到了短暂的延迟,但是当伽利略吩咐助手去往另一个两倍距离的位置,然后重复实验的时候,他们却没发现延迟的时间有所延长。显然,光传播的速度太快,跨越几英里需要的时间极短,他们观察到的延迟实际上是因为助手并未在看到灯光的同时立即打开遮光板——如今我们称之为反应延迟。
虽然伽利略的实验并未得到任何有意义的成果,但他的另一个发现却为人类真正首次测量光速奠定了基础——他发现了木星的卫星。1675年,丹麦天文学家罗默(Roemer)在观察木星卫星月食时发现,从卫星被木星的影子掩盖到它们重新出现,这中间的时间间隔并不是恒定的,有时候会长一点儿,有时候又会短一点儿,具体取决于当时木星和地球之间的距离。罗默立即意识到(正如你将在图31B中看到的一样),之所以会出现这种现象,并不是木星卫星的运行有什么异常,而只是因为木星和地球之间不同的距离带来了不同的延迟时间。通过他的观察,我们发现,光传播的速度大约是每秒185,000英里。难怪伽利略的实验怎么都测不出光速,因为灯笼发出的光只需要几十万分之一秒的时间就能在他和助手之间跑一个来回!
虽然伽利略的遮光灯笼过于粗糙,无法测量光速,但后来的科学家用更精密的物理仪器完成了这个任务。图31C向我们展示了法国物理学家斐索(Fizeau)首次采用的短距离测量光速的实验设备。这套装置的核心是安装在同一根轴上的两个钝齿轮,如果站在平行于轴的方向上观察,你会看到第一个齿轮的齿遮住了第二个齿轮的齿缝,所以无论你怎么摆弄这根轴,沿轴向传播的一小束光也无法穿透两层齿轮的阻隔。假设这套两个齿轮组成的系统正在飞速旋转,从第一个齿轮的齿缝中漏过来的光需要一定的时间才能到达第二个齿轮,如果在这段时间内,整套系统转动的距离等于齿距的一半,那么这束光就能透过第二个齿轮的齿缝传出去。这就像汽车在一条装有同步红绿灯系统的大道上行驶,只要速度合适,它一路遇到的都是绿灯。如果齿轮的转速增加一倍,那么当光线到达第二个齿轮时,轮齿会正好将它挡住。不过只要齿轮的转速继续增加,光线又会再次透过第二个齿轮,因为刚才挡光的轮齿已经离开了光传播的路径,这束光落到了下一个齿缝中。因此,我们只需要观察光线从出现到消失(或者反之)所对应的转速,就能估算光在两个齿轮间传播的速度。为了减少实验难度、降低齿轮转速,我们可以在两个齿轮之间增加几面镜子(如图31C所示),让光多传播一段距离。通过这个实验,斐索发现,当齿轮转速达到每秒1000转时,他首次观察到了透过齿缝的光。这意味着在光从第一个齿轮传到第二个齿轮的这段时间里,每个轮齿移动的距离等于齿距的1/2。每个齿轮各有50个完全相同的轮齿,因此这段距离等于齿轮周长的1/100,齿轮移动这段距离所需的时间等于其自转周期的1/100。有了这个数据,再加上光在两个齿轮之间传播的总距离,斐索最终计算得出,光的传播速度是每秒300,000千米,或186,000英里,这个数值和罗默观察木星卫星得出的结果差不多。
继这几位先驱之后,人们又做了很多天文学和物理实验来测量光速。目前真空光速(通常用字母“c”来指代)最准确的估算值是:
c=299,776千米/秒 或 186,300英里/秒。
光的速度极快,所以很适合用来度量天文距离;天文尺度的距离常常大得离谱,若用英里或者千米来表示的话,恐怕得写满好几页纸。因此,天文学家会说,某颗恒星和地球之间的距离是5“光年”,就像我们常说某个地点坐火车5小时能到。由于1年约有31,558,000秒,所以1光年等于31558000×299776=9460000000000千米,或者5,879,000,000,000英里。通过“光年”这个术语,我们将时间化作了一个实用的维度,时间单位也因此成为一个可用于度量空间的单位。反过来说,我们也可以创造另一个术语“光英里”,用它来描述光行经1英里的距离所需的时间。利用上面介绍的光速值,我们可以算出1光英里等于0.0000054秒。以此类推,1“光英尺”等于0.0000000011秒。上一节中我们讨论的四维立方体的问题也由此得到了解答。如果这个正立方体在空间中的边长是1英尺,那么它在时间维度上的跨度必然只有0.000000001秒。要是这个立方体存在的时间跨度足足有一个月,那么它看起来应该更像四维空间中的一根长棍,因为它在时间维度上的跨度比另外三个维度大得多。
3 四维距离
根据爱因斯坦最初的设想,我们只需推广一下毕达哥拉斯定理,就能算出四维距离;要研究事件之间的物理关系,四维距离是一个比独立的空间间隔和时间间隔更基本的值。
……
因此,基于上述讨论,既然我们认为空间距离永远是实数,而时间距离永远是纯虚数,那么或许可以说,实数的四维距离与普通空间距离的关系更为密切,而虚数四维距离与时间间隔的联系更紧密。用闵可夫斯基的术语来说,第一种四维距离叫作“类空距离”(spatial),第二种则是“类时距离”(temporal)。
在下一章中我们将看到,类空距离可以转化为普通的空间距离,而类时距离可以转化为普通的时间间隔。但是,这两种距离一个是实数,一个是虚数,二者之间有一道不可逾越的藩篱,所以它们无法互相转化,正是出于这个原因,我们不能将尺子变成时钟,反过来也不行。
第五章 空间和时间的相对性
1 时空互变
虽然在数学上将空间和时间统一在一个四维世界内的努力并未完全消弭空间距离与时间间隔的差异,但通过这样的尝试,我们的确发现空间和时间这两个概念具有高度的相似性,与爱因斯坦之前的时代相比,物理学由此迈出了一大步。事实上,现在我们必须将不同事件的空间距离和时间间隔视为这些事件的四维距离在空间轴和时间轴上的投影,所以只需要旋转这个四维坐标轴,或许我们就能将空间距离部分转化为时间间隔,反之亦然。但要旋转四维时空坐标轴,我们具体应该怎么做呢?
……
再举个例子,我们不妨设想一个人坐在行驶的火车餐车里吃饭。从餐车服务生的角度来看,从开胃菜到甜品,这个人在用餐过程中始终坐在同一个位置(靠窗的第三张桌子);但要是窗外的铁路旁有两名始终站在原地的扳道工——其中一名正好看到这位乘客吃开胃菜,而另一名正好看到他在吃甜品——那么从他们的角度来看,这两个事件发生的地点相距好几英里。所以我们或许可以说:某位观察者看到两个事件在不同的时刻发生在同一个地点,但另一位处于不同状态(或者不同运动状态)下的观察者可能认为这两个事件发生的地点并不相同。
从时空等价的角度来说,我们可以将上面这句话里的“时刻”和“地点”互换,得到一个新的说法:某位观察者看到两个事件在不同的地点同时发生,但另一位处于不同运动状态下的观察者可能认为这两个事件发生的时间并不相同。
将这个说法套用到餐车的例子里,我们就会看到,尽管服务生赌咒发誓说餐桌上相对而坐的两位乘客同时点燃了饭后的那支香烟,但站在铁路旁透过车窗向内张望的扳道工却坚决表示,其中一位先生点烟的时间就是比另一位早。
因此,某位观察者认为两个事件同时发生,但另一位观察者可能认为二者之间有一定的时间间隔。
四维几何学认为空间和时间只是恒定不变的四维距离在对应轴上的投影,因此我们必然得出上述结论。
2 以太风和天狼星之旅
现在我们不妨问问自己,如果只是为了满足运用四维几何学语言的愿望,就不惜彻底颠覆我们习以为常的经典时空观,这样做真的对吗?
……
不过要理解现在观察到的现象,应该有一个比“桌子收缩了”更简单的解释。的确,我们知道,物质在阻力较大的介质中行进时会产生一定的收缩。比如说,湖面上行驶的摩托艇会同时受到马达推力与湖水阻力的挤压,但这种机械收缩的程度取决于制造船体的材料的强度。受力相同的情况下,铁船产生的形变肯定小于木船。但无论迈克耳孙将实验装置放在哪里,都无法得到预想的结果,所以在这个实验中,物质的收缩似乎只跟运动速度有关,和材料强度毫无关系。不管安放实验装置的桌子是石头的,还是铸铁、木头或者其他任何材料,它们的收缩程度似乎始终如一。所以我们清晰地看到,这是一种普遍效应,它会导致所有运动物体以完全相同的程度收缩。或者换个说法,1904年,爱因斯坦教授曾这样描述我们刚才讨论的现象:这样的收缩来自空间本身,以相同速度运动的任何物体都会产生同样程度的收缩,这仅仅是因为它们都嵌在同一个收缩了的空间里。
前两章我们已经介绍了空间的很多特性,所以现在提出这样的说法也相当合理。为了加强理解,我们暂且将空间想象成一团弹性良好的果冻,不同物体的边界都嵌在里面。一旦空间因为挤压、拉伸或者扭转而变形,那么嵌在里面的所有物体的形状也会自动地发生相应的变化。空间变形引起物体变形和其他外力导致物体内部产生应力而变形,这是两种完全不同的情况,我们必须严格地将二者区分开来。图37所示的二维图像或许可以帮助你理解这个重要的区别。
……
不过,尽管物理世界很疯狂,但还没有那么疯狂,这样的黑魔法显然不可能存在,原因可以简单地归结为一句话:任何物体的运动速度都不可能达到或者超过光速。
这条基本公理的物理基础来自一个事实,无数实验直接证明了这一点:随着物体的运动速度趋近光速,它的惯性质量(这个值度量的是阻碍物体进一步加速的机械力)会趋近于无穷大。因此,如果一颗手枪子弹的速度达到了光速的99.99999999%,那么阻碍它进一步加速的力量(即子弹的惯性质量)相当于一颗直径12英寸的炮弹;要是它的速度达到光速的99.99999999999999%,那么这颗小子弹受到的内部阻力就等于一辆重载卡车。无论我们付出多大的努力试图推动这颗子弹,都永远无法征服最后的一位小数,使它的速度达到宇宙中所有运动的上限!
3 弯曲的空间和引力之谜
我得向可怜的读者道个歉,前面二十页介绍四维坐标系的内容肯定读得大家苦不堪言,现在我们不妨去弯曲的空间里散散步。大家都知道曲线和曲面,但“弯曲的空间”又是什么意思?想象弯曲空间之所以这么困难,倒不是因为这个概念有多么出奇,而是因为一个简单的事实:我们可以从外面观察曲线和曲面,但只能从里面观察三维空间的弯曲,因为我们自己身处其中。为了理解三维的人类如何设想自己生活于其中的空间的弯曲,首先我们还是想想生活在二维面上的影子生物。在图39a和39b中,我们可以看到,平坦和弯曲(球状)的“面世界”里的影子科学家正在研究他们所在的二维空间的几何学。当然,三角形是可供研究的最简单的几何图形,它由三条直线连接三个几何点构成。你们大概还记得高中几何课上讲过,平面上任何一个三角形的三个内角之和总是等于180°。不过我们也很容易看到,这条定理并不适用于球面上的三角形。事实上,球面上由两条从极点出发的地理经线和一条地理纬线组成的三角形,它的两个底角都是直角,而顶角可能是0°到360°之间的任何数字。比如图39b中那两位影子科学家研究的三角形,它的三个内角之和等于210°。所以我们可以看到,通过测量自己所在的二维世界里的几何图形,这些影子科学家不必从外面观察也能发现他们的世界是弯曲的。
将这种观察世界的方法移植到多一个维度的世界里,我们自然可以得出结论:生活在三维空间中的人类科学家不必跳出这个世界进入第四个维度,也能通过测量空间中连接三个点的直线之间的角度,确认我们的空间是否弯曲。如果三个角之和等于180°,那么空间是平坦的,否则它必然弯曲。
……
要完全理解爱因斯坦提出的弯曲空间理论以及它和万有引力基本问题之间的关系,现在我们只需要迈出关键的最后一步。首先我们必须记住,刚才我们讨论的三维空间只是代表了四维时空世界的一部分,后者才是容纳所有物理现象的舞台。因此,空间弯曲的特性必然反映了四维时空世界中更普遍的弯曲,代表我们这个世界的光线与物体运动的四维世界线在超空间中看起来一定是弯曲的。
从这个角度出发,爱因斯坦得出了一个重要的结论:引力现象只不过是四维时空世界的弯曲产生的效应。事实上,现在我们或许可以抛弃“太阳直接对行星产生引力,使之绕太阳作圆周运动”这个不准确的旧说法,更准确的描述应该是:太阳的质量弯曲了周围的时空,行星的世界线看起来之所以是图30中的样子,仅仅是因为,那个弯曲的空间中的测地线就是这样的曲线。
因此,“引力是一种独立的力”这个概念彻底从我们的推理中消失了,取而代之的是空间的纯几何概念:在这个因大质量物体的存在而产生弯曲的空间中,所有物体沿“直线”或者说测地线运动。
4 封闭空间和开放空间
这一章结束之前,我们还得简单讨论一下爱因斯坦时空几何学中另一个重要的问题:宇宙到底是有限的还是无限的。
第三卷 微观世界
第六章 下降的楼梯
1 希腊人的观点
首先提出这个问题并试图寻找答案的人是希腊哲学家德谟克利特(Democritus),他大约生活在两千三百年前的雅典。德谟克利特认为,这个问题的答案是否定的;他更愿意相信,无论某种物质看起来多么均匀,它也一定是由大量(但德谟克利特并不知道到底有多少)独立的极小的(他也不知道到底有多小)微粒组成的。对于这样的微粒,德谟克利特称之为“原子”或“不可分割之物”。不同物质包含的原子(或者不可分割之物)数量不同,但它们的区别只是表面的虚假现象。事实上,火原子和水原子完全相同,只是二者看起来不一样。确切地说,所有物质都由永恒不变的同样的原子组成。
但同时代一位名叫恩培多克勒(Empedocles)的人却提出了另一套观点,他认为原子分为几种,这些原子以不同的比例组合在一起,形成了千姿百态的物质。
基于当时粗浅的化学知识,恩培多克勒将原子分为四种,分别对应四种所谓的基本元素:土、水、气和火。
按照恩培多克勒的观点,土壤是土原子和水原子紧密结合在一起而形成的:二者结合得越好,土壤就越肥沃。从土壤中长出来的植物由土原子、水原子和来自阳光的火原子组成,这几种原子共同形成了复合木分子。干燥的木头失去了水原子,我们可以将木头燃烧的过程视为木分子重新分解成原来的火原子和土原子,前者随着火焰飘散,后者留存下来,成为灰烬。
2 原子有多大?
其实德谟克利特和恩培多克勒在讨论原子的时候都秉持着一个模糊的哲学理念:物质不可能无限分割成越来越小的碎片,我们最终必然抵达一个不可分割的最小单元。
3 分子束
研究透过小孔喷入周围空间的气体和蒸汽时,我们也可以顺便找到另一种揭示物质分子结构的有趣方法。
假设我们有一个真空的玻璃泡泡(图44),它的中央是一个小电炉:将电阻丝绕在带孔洞的陶制圆筒上,就能做出一个电炉。如果我们在电炉里放一小块低熔点金属,例如钠或者钾,那么它产生的金属蒸汽将填满圆筒内部,然后透过圆筒壁上的小孔释放到周围的空间中。这些蒸汽一旦接触玻璃泡冰冷的侧壁就会粘在上面,在球壁上的不同区域形成一层极薄的镜面,清晰地告诉我们金属蒸汽从电炉中喷出后的运动轨迹。
接下来我们还会进一步发现,电炉的温度会影响金属膜在球壁上的分布。电炉的温度越高,陶制圆筒内的金属蒸汽密度就越高,我们会看到蒸汽从小孔中喷射出来,就像水壶或蒸汽发动机“冒烟”一样。进入玻璃泡内部相对较大的空间以后,金属蒸汽会向四面八方扩散(图44a),充斥整个球体,在球壁上形成比较均匀的薄膜。
但要是电炉的温度比较低,陶制圆筒内部的蒸汽密度升不上去,我们就会观察到另一番景象。从小孔中喷出的金属蒸汽不再扩散,而是沿着直线运动,所以大部分金属膜最后都会落在玻璃泡正对圆筒孔洞的那一面上。如果在小孔前方放一块挡板(图44b),你会更清晰地观察到金属微粒的直线运动。挡板后方的玻璃壁上没有金属膜,最终会形成一块和挡板几何形状完全一致的透明斑。
如果你还记得蒸汽的成分是大量独立的分子,它们在空间中向四面八方运动,彼此不断碰撞,那么你应该很容易理解金属蒸汽在高低温下的表现为何大不相同。从小孔中喷出的高密度金属蒸汽就像急着逃离着火剧院的一大群人,冲出剧场大门以后,他们在街道上也会不断冲撞彼此,四散奔逃。但从另一方面来说,低密度蒸汽可以类比成每次只有一个人走出剧场大门,所以他大可以从容不迫地直线前进,不会被别人撞偏。
从电炉小孔中喷出的低密度蒸汽物质流被称为“分子束”,它由紧挨在一起穿过空间的大量独立分子组成。研究单个分子特性的时候,这样的分子束十分有用。比如说,你可以利用分子束来测量分子热运动的速度。
研究分子束速度的设备最初是由奥托·施特恩(Otto Stern)设计的,从本质上说,这套装置和斐索测量光速的设备(见图31)完全一样。它由两个安装在同一根轴上的齿轮组成,两个同轴齿轮以特殊的角度安装,要让分子束畅通无阻地穿过两个齿轮,这根轴必须以特定速度旋转(图45)。施特恩在轴的尽头放了一块隔板,用于接收透过齿轮的细分子束;利用这套设备,他发现一般来说,分子运动的速度很快(钠原子在200℃时的运动速度是每秒1.5千米),而且随着气体温度的升高,分子运动的速度还会进一步增大。这直接证明了热运动理论,根据这套理论,物体温度升高实际上是因为分子不规律热运动加剧。
4 原子摄影
虽然上述例子足以证明原子假说的正确性,但我们还是更相信“眼见为实”,所以要确凿无疑地证明原子和分子的存在,我们最好能让人类用肉眼看到它们。直到最近,英国物理学家W.L.布拉格(W.L.Bragg)才实现了这个目标,他设法拍下了几种晶体原子和分子的照片。
5 解剖原子
德谟克利特给原子起的名字来自希腊语中的“不可分割之物”,当时他认为,这些微粒代表了物质可分割的最小单元,换句话说,原子是组成所有物质的最小、最简单的结构组件。几千年后,“原子”这个古老的哲学概念得到了科学的支持,基于我们观察到的大量证据,原子不可分割的信念越来越根深蒂固,人们想当然地认为,不同元素的原子性质之所以各不相同,是因为它们的几何形状有所差异。比如说,他们认为氢原子的形状近似球体,而钠原子和钾原子就像拉长的椭圆。
从另一方面来说,在人们的想象中,氧原子看起来就像甜甜圈,中间有个近乎封闭的洞,所以将两个球状的氢原子一上一下同时填入氧原子中间的洞里,我们就得到了水分子(H₂O)。钠原子和钾原子之所以能够轻而易举地取代水分子中的氢原子,是因为比起球状的氢原子来,这两种长椭球形的原子更契合氧原子甜甜圈中间的洞。
从这个角度来看,不同元素之所以会释放不同的光谱,是因为不同形状的原子有不同的振动频率。于是物理学家试图通过元素释放的光谱倒推出不同原子的形状,但没有成功,这和我们从声学角度解释小提琴、教堂钟和萨克斯管音色的区别如出一辙。
但是以不同原子的几何形状为基础解释其化学和物理特性的努力全都收效甚微,直到人们认识到,原子并不是几何形状各不相同的基本粒子,恰恰相反,它是由大量独立运动部件组成的相当复杂的装置,我们才真正迈出了理解原子特性的第一步。
解剖精致的原子是一项复杂的手术,首次完成这一壮举的是著名的英国物理学家J.J.汤姆孙(J.J.Thomson),他成功证明了各种化学元素的原子由带正电和负电的部件组成,电磁力将这些部件结合在一起。按照汤姆孙的设想,原子其实是一团均匀的正电荷,大量带负电的粒子漂飘浮其中(图48)。负电粒子(汤姆孙将之命名为“电子”)携带的负电荷等于包裹它的正电荷,所以原子整体呈电中性。不过,由于电子与原子的结合相对比较松散,所以偶尔会有一个或者几个电子散逸出去,留下一个带正电的不完整的原子,也就是正离子。从另一方面来说,有时候原子又会从外部额外获取几个电子,于是它就得到多余的负电荷,变成了负离子。原子得到多余正电荷或负电荷的过程被称为离子化。汤姆孙的观点基于迈克尔·法拉第(Michael Faraday)的经典著作,后者证明了原子携带的电量必然等于一个基本量的倍数,这个基本电量单位的值是5.77×10−10。但比起法拉第来,汤姆孙又向前走了一大步,他提出原子电量之所以总是成倍变化,是因为这些电荷实际上是独立的微粒;除此以外,他还找到了从原子中分离电子的方法,甚至开始研究空间中高速飞行的自由电子束。
汤姆孙研究自由电子束的一大成果是估测电子的质量。他利用强电场从灼热电线之类的材料中分离出一束电子,然后让它穿过两片带电电容板之间的空间(图49)。由于这束电子携带负电荷——或者更准确地说,它本身就是负电荷——所以它会被电容正极吸引,同时被负极排斥。
如果在电容后面放一块荧光屏,我们很容易就能观察到电子束的偏转。知道了单个电子的电量和它在特定电场中的偏转程度,就能估算出电子的质量,于是我们发现,电子真的很轻。事实上,汤姆孙发现,单个电子的质量只有氢原子质量的1/1840,这意味着原子质量主要来自带正电的组件。
虽然汤姆孙正确地预见到了原子内部有大量运动的带负电的电子,但他认为原子内部的正电荷是均匀分布的,这个观点却错得有点儿离谱。1911年,卢瑟福证明了贡献原子大部分质量的正电荷实际上集中在原子中央一个非常小的原子核里。这个结论来自他的一个著名实验,这个实验的目的是研究所谓的“阿尔法(α)粒子”穿过物质时是否会发生散射。α粒子是特定不稳定元素(例如铀或镭)的原子自发分裂而释放的高速微粒,科学家已经证明了α粒子的质量近似原子的质量,而且它携带正电荷,所以它一定就是原子中带正电的组件。α粒子穿过目标材料的原子时会被其内部的电子吸引,同时被正电组件排斥。不过,由于电子实在太轻,所以它们无法影响入射α粒子的运动,就像一大群蚊子也不可能影响受惊飞奔的大象。但从另一方面来说,由于原子中携带正电的组件与入射α粒子的质量相当,所以只要二者的距离够近,前者必然影响后者的运动,使之偏离原有轨道,向着四面八方散射。
卢瑟福用一束α粒子照射一片铝箔,然后惊讶地发现,要解释他在实验中观察到的结果,就必须假设入射α粒子与原子正电组件之间的距离不到原子直径的千分之一。当然,要满足这样的条件,唯一可能的解释是,入射α粒子和原子正电组件的尺寸都只有原子的几千分之一。卢瑟福的发现推翻了汤姆孙“正电荷均匀分布”的原子模型,他的新理论认为,尺寸极小的原子核位于原子中央,周围环绕着一大群带负电的电子。现在的原子不再是西瓜的形状(电子就是西瓜籽),看起来倒更像是缩微版的太阳系,原子核类似太阳,电子类似行星(图50)。
原子和太阳系不仅结构相似,还有其他很多共同点:原子核的质量相当于原子总质量的99.97%,而太阳系99.87%的质量都集中在太阳里;围绕原子核运行的电子之间的距离相当于电子直径的几千倍,太阳系内行星间的距离与行星直径的比值差不多也是这个数。
不过,二者最重要的相似之处在于,原子核和电子之间的电磁力与距离的平方成反比,太阳和行星之间的引力也遵循同样的数学规律。所以电子沿圆形和椭圆形轨道绕着原子核运动,就像太阳系里的行星和彗星一样。
根据原子内部结构的上述理论,不同化学元素的原子之所以有所区别,原因必然是不同原子内部绕核运动的电子数量不同。由于原子整体呈电中性,绕核运动的电子数量必然等于原子核携带的正电荷数量,根据α粒子因原子核的排斥而产生的偏移散射,我们又能直接估算出原子核携带的正电荷数量。于是卢瑟福发现,如果将所有化学元素按照从轻到重的顺序排列起来,那么每一种元素的原子包含的电子数都比前一种元素多一个。这样一来,氢原子只有1个电子,氦原子有2个电子,锂有3个,铍有4个,以此类推,直到最重的自然元素铀,它一共拥有92个电子。
原子在这个序列中的排位通常被称为该元素的原子序数,根据元素的化学性质,化学家编制了一张化学元素周期表,这张表格中的原子编号和位置也和它的序数保持一致。
这样一来,任何一种元素的物理性质和化学性质都可以简单地用绕核旋转的电子数量来表示。
19世纪末,俄国化学家D.门捷列夫(D.Mendeleev)注意到,自然序列中的元素化学性质呈现出明显的周期性。他发现,这些元素的性质每隔一定数目就会重复一次。图51生动地体现了这样的周期性,在这幅图中,代表已知元素的所有符号沿着圆筒表面排成了一条螺旋状的带子,拥有类似性质的元素都落在同一列里。我们看到,第一组元素只有2种:氢和氦;接下来的两组分别包含了8种元素;最终元素性质的重复周期扩大到了18种。如果你还记得,自然序列中每种元素的原子都比前一种多一个电子,那么我们必将得出一个无法回避的结论:元素的化学性质之所以会呈现出明显的周期性,这必然是因为原子内部的电子——或者说“电子层”——拥有某种重复出现的稳定结构。第一层最多能容纳2个电子,接下来的两层分别能容纳8个电子,再往外的电子层最多能容纳18个电子。通过图51我们还会发现,元素的自然序列进入第六个和第七个周期以后,元素性质严格的周期律似乎被打乱了,这一块的两组元素(所谓的稀土元素和锕系元素)必须抽取出来单独放到一边。之所以会出现这样的异常现象,是因为这些元素原子内部的电子层结构比较特殊,从而影响了它们的化学性质。
元素周期性排列形成的螺旋条带,元素性质的重复周期分别是2、8 和18。下方的示意图单独画出了扰乱元素“周期环”的两组异常元素(稀土元素和锕系元素)。
既然我们已经知道了原子的模样,现在我们可以找找这个问题的答案了:是什么样的力将不同元素的原子结合在一起,形成各种各样的复杂化合物分子?比如说,钠原子和氯原子为什么会结合形成食盐分子?我们可以在图52中看到,氯原子的第三个电子层少了一个电子,而钠原子在填满第二个电子层以后,正好有一个多余的电子。所以来自钠原子的多余电子必然倾向于与氯原子结合,填满后者的第三个电子层。失去了一个电子(带负电荷)的钠原子带正电,与此同时,得到一个电子的氯原子带负电。在电磁力的吸引下,两个带电原子(或者说离子)结合起来形成氯化钠分子,俗称食盐。以此类推,氧原子的最外层少了两个电子,所以它会从两个氢原子处分别“绑架”一个电子,形成一个水分子(H₂O)。换句话说,氧原子通常对氯原子没兴趣,氢原子和钠原子也很难擦出火花,因为前面那两个家伙都劫掠成性,不习惯付出,与此同时,后面的两种原子都对掠夺没兴趣。
氦、氩、氖、氙等电子层完整的原子既不需要夺取也不必付出多余的电子,它们更喜欢自己跟自己玩,所以这些元素(所谓的“稀有气体”)化学性质很不活泼。
这个小节我们主要介绍了原子和它的电子层,本节结束之前,我们还得讨论一下原子携带的电子在金属类物质中扮演的重要角色。金属和其他材料很不一样,因为金属原子内部的外层电子与原子核的结合十分松散,所以常常会有一两个电子挣脱原子核的束缚,成为自由电子。这样一来,金属材料内就有大量漫无目的游荡的自由电子,就像一群无家可归的流浪汉。如果给金属丝通电,这些自由电子会顺着电压的方向狂奔,形成我们所说的电流。
金属之所以拥有优秀的导热性能,也是因为自由电子的存在——但这部分内容我们留到后面的章节再讲。
6 微观力学与不确定性原理
如前所述,原子内部绕核旋转的电子系统类似行星系,所以我们自然会认为,电子的运动也应该遵循行星绕日运动的天文规律。再说得具体一点儿,由于电磁定律和引力定律十分相似——电磁力和引力都跟距离的平方成反比——我们难免觉得,原子内部的电子必然沿椭圆轨道围绕原子核运动(图53a)。
但是任何试图借助太阳系天体运动规律来描绘原子内部电子运动的努力最终总会出乎意料地一败涂地,以至于人们一度怀疑,要么是物理学家疯了,要么是物理学本身出了问题。麻烦的根源在于,和太阳系的行星不一样,原子内部的电子携带电荷;和任何振动或旋转的带电粒子一样,绕核旋转的电子必然释放大量电磁辐射。这些辐射会带走能量,那么合理的推测是,原子内部的电子会沿着一条螺旋形的轨道(图53b)不断逼近原子核,等到旋转动能彻底耗尽,它最终会坠落到原子核上。电子携带的电量和旋转频率都是已知的,根据这些数据,我们可以轻松算出,电子失去所有能量坠向原子核,这个过程消耗的时间最多只有百分之一微秒。
因此,根据已有的物理学知识,如果原子内部的结构真的和行星系一样,那么它只能维持亿万分之一秒的时间,换句话说,这样的原子旋生旋灭,根本无法长期存在。
但是尽管我们从理论上推出了如此悲观的前景,但现实却告诉我们,原子结构非常稳定,原子内部的电子高高兴兴、不知疲倦地绕着中央的原子核绕圈,绝不损失任何能量,更没有坠落的迹象!
这怎么可能!我们试图运用完善的旧理论来解释原子内部的电子运动,为什么会得出与现实大相径庭的结果?
要回答这个问题,我们必须回顾科学中最基本的问题:什么是“科学”?科学的本质是什么?什么又是事物的“科学解释”?
我们不妨从记忆中找个简单的例子,比如说,古希腊人相信地球是平的。你很难责怪他们,因为要是你走进一片旷野,或者在开阔的水面上航行,你也会亲眼见证,除了山峦偶尔的起伏以外,地球表面看起来的确是平的。古人的错误不在于他们断然宣布“某人在给定观察点看到的地球是平的”,而在于他们贸然将这一结论推广到了实地观察的范围以外。事实上,只要做一些超出日常经验范围的观察,譬如说研究月食期间地球投在月面上的影子,或者麦哲伦著名的环球航行,我们立即可以证明,这样的推广是错误的。现在我们说,地球看起来是平的,这只是因为我们只能看到地面上很小的一部分。还有一个类似的例子,我们在第五章中讨论过,宇宙中的空间可能是弯曲有限的,尽管从我们有限的观察范围来看,宇宙十分平坦,而且广袤无垠。
不过,我们想要讨论的明明是组成原子的电子实际运动与理论预测的矛盾,刚才说的一大堆和这个问题有什么关系?答案是,在这样的研究中,我们首先默认了电子运动遵循的规律与大型天体完全一致,或者更确切地说,与我们日常生活中习惯的“正常尺寸”的物体完全一致,所以我们才会用同一套术语描述它们。事实上,我们熟悉的力学定律和概念都是基于已有的观察经验建立起来的,而这些经验都来自与人类自身尺寸相仿的物体。后来我们开始运用这些规律解释另一些大得多的物体的运动,例如行星和恒星,结果获得了成功,所以我们才能极为准确地计算前后几百万年的各种天文现象。因此,我们毫不怀疑,这些熟悉的力学定律确实可以向外推广,解释大型天体的运动。
尽管经典力学定律的确能解释巨型天体、炮弹、钟摆和玩具陀螺的运动,但电子的大小和质量只相当于最小的力学设备的亿万分之一。我们凭什么相信,同样的定律就一定适用于它呢?
当然,我们没有理由预先假设经典力学定律就一定无法解释原子内部细微部件的运动;但是从另一方面来说,如果真的遭遇了这样的失败,我们也不必过于惊讶。
这样一来,既然天文学定律与电子的实际运动产生了矛盾,那么我们首先应该考虑,运用经典力学来解释这类尺寸极小的粒子运动时,一些基本的概念和定律或许可以做些变通。
经典力学的基本概念包括粒子运动的轨道和粒子沿轨道运动的速度。在任意给定时刻,运动的物质粒子必然占据空间中一个确定的点,物质粒子在不同时刻占据的点串联起来,就形成了它的运动轨道,这句话通常被视为不言自明的真理,它也是我们描述物体运动的基础。如果知道特定物体在两个不同时刻占据的位置之间的距离,再除以这两个时刻的时间间隔,就能算出该物体的运动速度。位置和速度,这两个概念奠定了整个经典力学的根基。直到不久前,恐怕还没有哪位科学家想到过,描述运动现象的这两个最基本的概念竟然会有瑕疵,要知道,从哲学的角度来说,这两个概念完全是先验的。
但是科学家运用经典力学定律描述微小的原子系统内部运动的努力却遭遇了彻底的失败,于是我们意识到,在这种情况下,有的东西可能彻底错了;人们越来越怀疑,这样的“错误”可能存在于经典力学最基本的层面。对于原子内部的微小部件来说,物体的连续运动轨道和任意给定时刻的速度,这些基本概念似乎显得过于粗糙。简单地说,将我们熟悉的经典力学理论推广到极小质量物体的运动中,这种不成功的努力告诉我们,要完成这个任务,我们必须对固有的概念做出极大的调整。但是如果经典力学的旧理念真的不适用于原子世界,那么在描述更大物体的运动时,它也不可能绝对正确。因此我们得出结论:经典力学理论只是非常近似“真理”的赝品,一旦我们试图用它来描述更精密的系统,就会遭遇惨痛的失败。
通过研究原子系统的力学特性、构建所谓的量子力学,我们为科学引入了全新的元素。量子力学基于科学家发现的一个事实:两个不同物体之间的任何相互作用存在一个确定的下限。这个发现彻底颠覆了“物体运动轨道”的经典定义。事实上,如果说运动物体必然拥有一条数学意义上的精确轨道,那就意味着我们有可能利用某种专门的物理设备来记录它的运动轨道。但是千万别忘了,记录轨道的行为必然干扰物体的运动;事实上,根据牛顿的作用力与反作用力定律,如果运动物体对记录其在空间中连续位置的测量设备产生了某种影响,那么这台设备必然对它产生反作用力。按照经典物理的假设,两个物体(此处指的是运动物体和记录其运动的设备)的尺寸不受限制,可以任意缩小,那么我们或许可以设想一种非常灵敏的理想设备,它既能记录运动物体的连续位置,又完全不会干扰后者的运动。
但是物理相互作用下限的存在彻底改变了讨论的前提,现在我们不能再随心所欲地削弱测量设备带来的干扰。这样一来,观察对运动的干扰变成了运动中不可或缺的一部分,物体运动的轨道也不再是数学意义上无限细的一条线,我们不得不将它视为空间中有一定厚度的弥散的条带。经典物理中数学意义上的清晰轨道变成了新力学里弥散的宽条。
不过,物理相互作用的最小量——它更常用的名字是“作用量子”(quantum of action)——是一个非常小的值,只有在研究极小物体的运动时才有意义。比如说,虽然手枪子弹的运动轨道并不是数学意义上的清晰线条,但这条轨道的“厚度”比组成子弹的物质原子尺寸小很多个数量级,所以实际上我们可以将它视为零。不过,如果将研究对象换成更容易被测量干扰的更轻的物体,我们就会发现,运动轨道的“厚度”变得越来越重要。对于绕核运动的电子来说,运动轨道的厚度与其直径尺度相当,所以我们不能像图53一样用线条来描绘电子的运动,而只能把它画成图54所示的样子。在这种情况下,我们不能再用经典力学中那些熟悉的术语来描述粒子的运动,它的位置和速度必然具有一定的不确定性(海森堡的不确定性原理和玻尔的互补原理)。
新物理学将我们熟悉的很多概念一股脑地扔进了废纸篓,什么运动轨道、绝对位置,还有运动粒子的速度,这样的进展过于惊人,我们简直觉得艰于呼吸。既然不能再用这些曾经被公认的基本原理研究原子内部的电子,那我们该用什么基础工具来理解电子的运动呢?为了应对量子力学中位置、速度、能量等参数的不确定性,我们需要一套取代经典力学方法的数学体系。
第七章 现代炼金术
1 基本粒子
各种化学元素的原子实际上都是大量电子绕核旋转形成的相当复杂的力学系统,知道了这一点以后,我们难免会问,那么原子核就是不可分割的最基本的物质单位吗?还是说它仍能进一步分割成更小、更简单的部件?92种不同的原子是否有可能进一步拆分成几种非常简单的粒子?
……
物理世界里的这些基本部件相互依赖,以各种方式结合在一起。因此,中子可以释放一个负电子和一个中微子,变成一个质子(中子→质子+负电子+中微子);质子也可以释放一个正电子和一个中微子,重新变成一个中子(质子→中子+正电子+中微子)。两个电性相反的电子可以转化成电磁辐射(正电子+负电子→辐射),反过来说,辐射也能创造一对电子(辐射→正电子+负电子)。最后,中微子能与电子结合,形成我们在宇宙射线中观察到的不稳定的介子,它还有一个不太恰当的名字,“重电子”(中微子+正电子→正介子;中微子+负电子→负介子;中微子+正电子+负电子→中性介子)。
中微子和电子的结合体携带大量内能,所以它的质量大约是两种粒子质量之和的100倍。
我们在图62中列出了组成宇宙结构的基本粒子示意图。
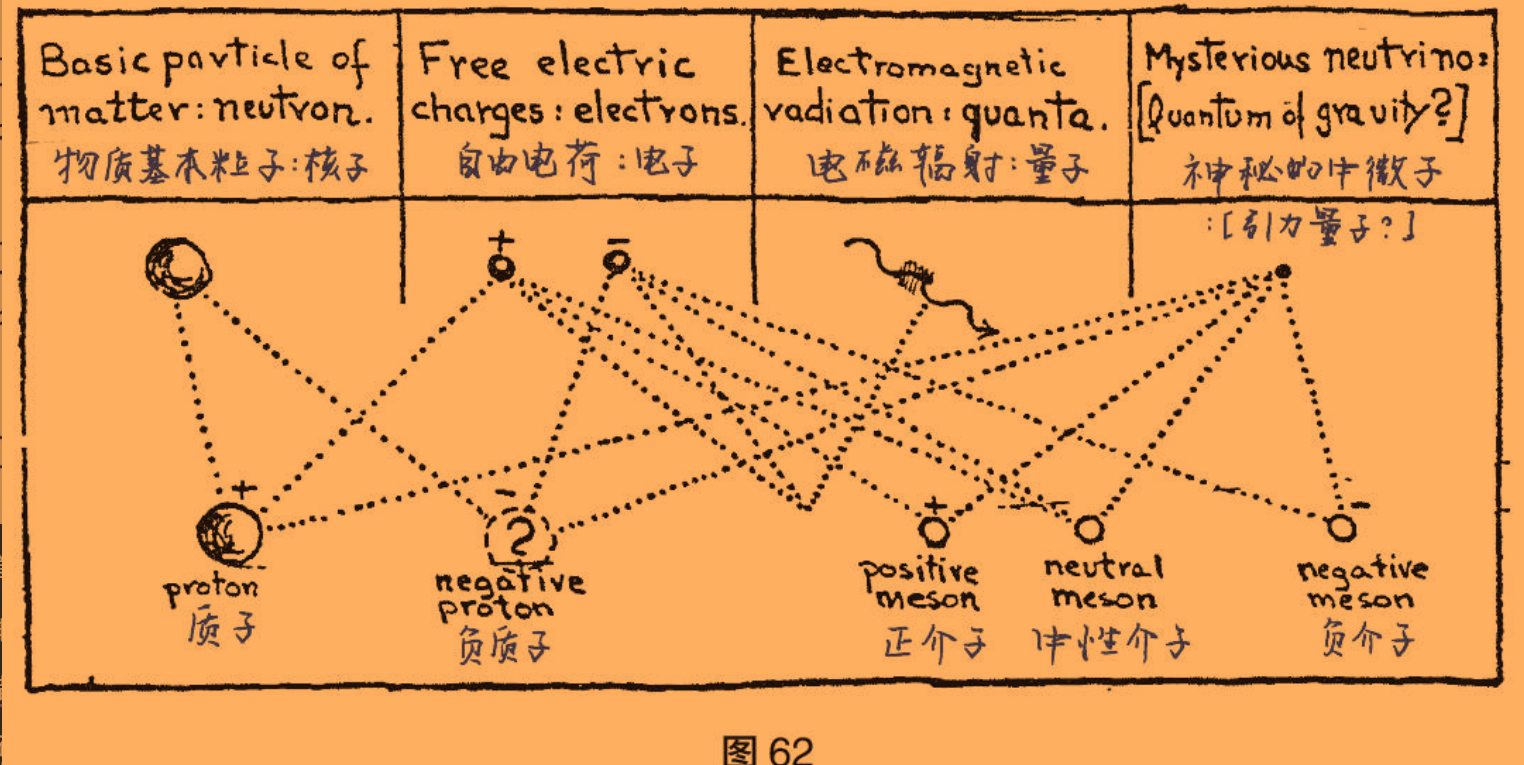
现代物理学的基本粒子名录以及这些基本粒子形成的各种组合
“不过这就算结束了吗?”你或许会问,“我们凭什么宣称核子、电子和中微子就是真正的基本粒子,无法再分割成更小的组件?要知道,仅仅半个世纪以前,我们还以为原子不能再分割了呢!瞧瞧今天的原子结构有多复杂!”我们当然无法预测物理学未来的发展,不过现在,我们有充分的理由相信,核子、电子和中微子就是真正的基本粒子,它们无法进一步分割。因为从化学、光学和其他角度来看,曾经被认为不可分割的原子性质相当复杂,而且各不相同,但现代物理学的基本粒子性质非常简单;事实上,它们和几何意义上的点一样简单。此外,经典物理学中“不可分割的原子”种类繁多,但现在我们只有三种基本粒子:核子、电子和中微子。尽管科学家付出了极大的努力,试图揭示万物最简单的本质,但他们终究不能化有为无。因此,我们对物质基本元素的探索之路似乎真的走到了尽头。
2 原子之心
既然我们已经全面认识了参与构造物质的基本粒子的特征和性质,那么现在,我们或许可以开始更深入地研究原子核,它是每个原子的心脏。从某种程度上说,原子的外层结构类似微型行星系,但原子核本身的内部结构却完全是另一幅图景。首先我们必须明确一件事:将原子核的各个部件结合在一起的力绝不仅仅是电磁力,因为组成原子核的粒子有一半(中子)完全不带电,而另一半(质子)携带正电,所以后者必然互相排斥。如果这些粒子之间只存在斥力,那它们肯定没法组成稳定的结构!
因此,要理解原子核内的各个组件为何能结合在一起,我们必须假设这些粒子之间存在另一种力,而且它是一种能够同时作用于带电和不带电核子的引力。这种无视粒子本身特性的引力通常被称为“内聚力”(cohesive force),比如说,普通液体分子就是靠内聚力结合在一起的,所以它们才不会四下飞散。
原子核内部的独立核子之间也存在类似的内聚力,所以原子核才不会被质子之间的斥力拆散。这样一来,在内聚力的作用下,原子核内的核子像罐头里的沙丁鱼一样紧紧挤在一起;而原子核外又是另一番景象:核外的电子分为好几层,每个电子都有充足的活动空间。本书作者首次提出了一个观点:我们可以认为原子核内部的组件排列方式类似普通液体分子。和普通液体一样,我们在原子核里也看到了重要的表面张力现象。或许你还记得,液体之所以会产生表面张力,是因为液体内部的粒子同时受到各个方向邻居的拉力,而表面的粒子受到的只有指向液体内部的拉力(图63)。
3 轰击原子
虽然原子质量的整数特性为原子核的复杂结构提供了有力的证据,但要彻底证明原子核的确拥有这样的复杂结构,我们必须设法将原子核分解成两个或者更多的独立部件,才能获得最直接的证据。
50年前(1896年),贝可勒尔(Becquerel)发现了放射性的存在,我们由此第一次看到了分裂原子的可能性。事实上,人们发现,靠近元素周期表尽头的元素(例如铀和钍)释放的高穿透性射线(类似普通X射线)来自原子缓慢的自发衰变。科学家深入研究了这些新发现的现象,很快得出结论:重原子核会自发衰变,分裂成两个相差悬殊的部件。(1)其中一个部件非常非常小,人们称之为α粒子,其实它就是氦原子核;(2)失去α粒子的原子核残骸成了新形成的子元素原子核。初始铀原子核分裂释放α粒子,残余的子元素原子核被称为铀XI;后者经历了内部电荷调整过程以后会释放2个自由负电荷(普通电子),变成铀同位素的原子核,它比初始的铀原子核轻4个单位。接下来,释放α粒子的裂变过程和释放电荷的调整过程循环重复,最终我们得到了铅,这种元素的原子核看起来十分稳定,不会继续衰变。
我们在另外两组放射性元素中也观察到了这种交替释放α粒子和电子的连续放射性反应:以重元素钍为首的钍系元素和以锕-铀为首的锕系元素。这三组元素都会自发衰变,最终只剩下铅的三种同位素。
4 核物理学
“核物理学”这个术语其实很不准确,但和其他很多以讹传讹的词语一样,我们对此毫无办法。既然“电学”描述的是自由电子束应用这个广阔领域的知识,那么以此类推,“核物理学”也应该是一门研究核能大规模释放的应用科学。我们在前几节中已经看到,各种化学元素(除了银以外)的原子核都携带着大量内能,这些能量可以通过聚变(较轻的元素)或裂变(较重的元素)的形式释放出来。我们还知道,人工加速带电粒子轰击原子核的方法虽然的确为各种核反应的理论研究带来了极大的便利,但我们却不能指望大规模实际应用这种方法,因为它的效率实在低得离谱。
既然从本质上说,α粒子、质子等普通粒子之所以效率低下,是因为它们带电,所以它们在穿过原子时会损失能量,因而无法有效靠近靶标材料的带电原子核。那么你肯定觉得,不带电的高速粒子效果应该更好,我们可以用中子轰击各种原子核。但新的问题又冒了出来!因为中子能够轻而易举地穿透原子结构,所以自然界并不存在自由中子;就算我们利用某种入射粒子人为地从原子核中轰出一个自由中子(比如说,α粒子轰击铍原子核就能产生一个中子),它也不会存在太长时间,周围的其他原子核很快就会重新将它捕获。
因此,要制造出轰击原子核的强大中子束,我们必须设法释放某种元素原子核内的所有中子。要达到这个目标,我们又绕回了低效带电粒子的老路。
不过,还有一个办法可以跳出这个怪圈。如果能够设法用中子轰击靶标原子核产生中子,而且每次裂变产生的子代中子数量大于初始中子,那么这些粒子就会像兔子(见第九章第2节,图97)或被感染组织内的细菌一样繁殖。一个中子在极短的时间内就能产生数目可观的后代,足以轰击一大块靶标材料的每一个原子核。
正是因为人们发现了这样一种能让中子以几何级数增殖的特殊核反应过程,才引发了物理学领域的一场大爆炸。原本只是研究物质最本质特性的核物理学也因此走出了科学肃静的象牙塔,卷入了报纸头条、狂热的政治讨论、大规模工业生产和军事研发的喧嚣的旋涡。读报的人都知道,铀原子核的裂变会释放出核能(它更常见的名字是“原子能”),直到1938年,哈恩(Hahn)和斯特拉斯曼(Strassman)才发现了这种核反应过程。但要是你以为裂变本身(即重原子核分裂成两个大致相同的部件的过程)能够促进核反应的发生,那就大错特错。事实上,裂变产生的两块核碎片都携带大量电荷(每块碎片携带的电荷约等于初始铀原子核的一半),所以它们无法靠近其他原子核;这些碎片很快就会在周围原子的电子层中消耗掉极高的初始能量,进入静止状态,无法制造下一步裂变。
对于可自发持续的核反应来说,裂变过程之所以那么重要,是因为人们发现,原子核裂变产生的每一块碎片在停止运动之前都会释放一个中子(图73)。
裂变过程之所以会产生这种特殊的余波,是因为重原子核的两块碎片诞生时伴随着剧烈的振动,就像断成两截的弹簧一样。这样的振动不足以引发次级裂变(每块碎片再次一分为二),但却足以导致其内部的某些结构单元与本体分离。我们说每块碎片释放出一个中子,这只是一个统计学角度的笼统说法;事实上,一块碎片有时候会释放出两个甚至三个中子——有时候又一个都没有。当然,每块裂变碎片释放中子的平均数量取决于振动的剧烈程度,而后者又取决于初始裂变过程释放的总能量。正如我们之前看到的,越重的原子核裂变产生的能量越多,那么元素周期表中位置越靠后的原子核裂变碎片产生的中子肯定也越多。这样一来,金原子核裂变(我们还没有实现这个过程,因为它需要的初始能量太高)碎片释放的中子平均数量肯定比1小得多,铀核裂变碎片释放中子的平均数约等于1(每次裂变大约释放2个中子),对于那些更重的元素(例如钚)来说,平均每块碎片释放的中子数量可能大于1。
要让中子自发增殖,100个入射中子显然应该制造出100个以上的子代中子。特定种类的原子核在裂变后产生中子的效率,即每次裂变平均生成的中子数量决定了它能否满足这个条件。千万别忘了,虽然中子轰击原子核的效率远高于带电粒子,但也达不到100%。事实上,这样的可能性永远存在:进入原子核的高速中子只将自己的一部分动能传递给了原子核,然后带着剩余的能量逃走了。在这种情况下,中子携带的能量分配给了几个原子核,每个原子核得到的能量都不足以引发裂变。
根据原子核结构的通用理论,我们可以得出一个结论:元素的原子量越大,它释放的中子引发核裂变的效率就越高,周期表尽头的那些元素裂变效率接近100%。
第八章 无序的规律
1 热无序
倒一杯水,仔细观察,你会看到一杯清澈的均匀液体,它的内部似乎不存在任何结构或者运动。(只要你别晃它!)但我们知道,水的均匀一致只是一种表面现象,如果将这杯水放大几百万倍,你将看到大量水分子紧紧挤在一起,形成粗粝的颗粒结构。
在同样的放大倍数下,你还会看到水的内部并不平静,水分子时时刻刻都在剧烈运动、彼此推搡,就像狂热的人群。水分子——或者说所有物质分子——的这种不规律运动被称为热运动,因为它直接表现为热现象。虽然人类的眼睛既看不到分子也看不到分子的热运动,但这种运动会对人体神经纤维产生一种特定的刺激,让我们感觉到“热”。对于那些比人类小得多的生命体(譬如悬浮在水滴中的细菌)来说,热运动带来的影响就大得多了,来自四面八方的躁动分子一刻不停地推挤、踢打这些可怜的小生物,让它们不得安宁(图77)。这种有趣的现象被称为布朗运动。一百多年前,英国植物学家罗伯特·布朗(Robert Brown)在研究细小的植物孢子时首次注意到了这种现象,布朗运动因此而得名。这是一种普遍存在的运动,悬浮在任意液体中的足够小的任意微粒都会产生布朗运动,空气中悬浮的烟雾和尘埃微粒也会表现出同样的性质。
2 我们该如何描述无序运动?
既然热运动完全没有规律,那我们岂不是完全没法用物理语言来描述它?如果你真的这样以为,那就错得太离谱了。事实上,热运动完全无规律的特性正好能用一种新定律来描述,我们称之为无序定律,或者统计行为定律。
3 计算概率
上面几个关于扩散的例子只是我们运用概率统计定律解决分子运动问题的简单范例。接下来我们将做进一步的讨论,试图理解最重要的熵增定律,它规范了所有物体的热行为,从微不足道的液滴到恒星组成的庞大宇宙;不过在此之前,我们需要先学习一下如何计算或简单或复杂的不同事件的概率。
4 “神秘的”熵
上面这几个计算概率的例子都和实际生活密切相关。我们从中学到,根据概率预测事件结果,这种方法在样本数量较少时常常令人失望,但试验次数越多,它就越准确。所以概率定律特别适合用来描述数量近乎无限的原子和分子,要知道,我们能够方便操控的最小的物体都包含着亿万个这样的粒子。因此,虽然统计学定律在描述醉鬼走路的时候只能给出一个近似的结果,因为案例中的醉鬼只有半打,他们每个人可能只会转二三十次弯;但如果将同样的定律应用于每秒钟都会碰撞几十亿次的几十亿个染色分子,我们却能得出最精准的物理学扩散定律。我们还可以说,起初只溶解于试管内一半水中的染料之所以倾向于均匀扩散到所有溶液中,是因为相对于初始状态而言,这样的均匀分布出现的概率更大。
正是出于同样的原因,此时此刻,就在你坐着读书的这间屋子里,从墙壁到墙壁、从地面到天花板都充斥着均匀的空气;你连想都不会去想,房间中的空气有可能突然自发聚集到某个遥远的角落里,让坐在椅子上的你窒息而死。但是从物理学的角度来说,这么可怕的事情并不是绝不可能发生,只是概率很低。
5 统计涨落
通过上一节的讨论,你应该明白,熵增定律及其所有推论完全基于一个事实:宏观物理世界中的所有物体都由大量独立分子组成,由于样本数量极多,我们做出的所有预测都拥有极高的精准度,几乎可视为百分百准确。但是如果物质的量非常非常少,这样的预测就没那么靠得住了。
第九章 生命之谜
1 我们由细胞组成
讨论物质结构的时候,我们暂时跳过了数量相对较少但非常重要的一个组别,这些造物迥异于宇宙中的其他所有物体,因为它们是活的。生命体和非生命体之间的重要区别到底是什么?基本物理法则成功地解释了非生命物质的性质,但它能解释生命现象吗?
说起生命现象,我们想到的通常是一些相对比较大、比较复杂的生命体,比如说一棵树,一匹马,或者一个人。但是要想研究生命体的基本性质,如果你试图从这些复杂的有机系统入手,那恐怕会徒劳无功,就像你没法通过汽车之类的复杂机械研究无机物的结构。
如果你非要这样做,那肯定会遇到很多困难,因为飞驰的汽车由数千个形状各异的部件组成,每个零件的原材料及其物理状态各不相同,其中有的是固体(例如钢质底盘、铜线和挡风玻璃),有的是液体(例如水箱里的水,油箱里的汽油,还有机油),有的是气体(例如化油器喷进汽缸的混合物)。要分析汽车这么复杂的物体,我们首先必须将它分解成物理成分均匀的独立部件。于是我们发现,汽车的成分包括金属(钢、铜、铬等)、多种玻璃状材料(玻璃和汽车结构中的塑性材料)、均匀液体(水和汽油)等等。
利用现有的物理学研究方法继续深入探查,我们发现汽车上的铜质零件由许多独立的细小晶体构成,这些晶体是由普通铜原子紧靠在一起、层层堆叠而成的;水箱里的水其实是许许多多的水分子,它们之间的联系相对比较松散,每个水分子由一个氧原子和两个氢原子构成;通过阀门进入汽缸的燃烧剂则是氧分子、氮分子和汽油分子的气态混合物,而汽油分子又由碳原子和氢原子组成。
同样地,分析复杂生命体(例如人体)的时候,我们也必须先将它分解成独立的器官,例如大脑、心脏和胃,然后再将这些器官拆分成生物性质均匀的原材料,这些材料有一个共同的名字:组织。
从某种意义上说,各种组织形成复杂生命体的原理类似我们用物理性质均匀的各种物质制造机械装置。从这个角度来看,研究各种组织的特性来分析生物整体功能的解剖学和生理学其实类似工程学,后者所做的也是根据我们所知道的原材料的机械、电磁和其他物理性质来研究各种机械的功能。
所以要解开生命之谜,我们要做的不仅仅是研究组织如何组成复杂生命体,还得进一步探查各种各样的原子如何形成组织,进而组成每一个活生生的生命。
如果你认为生物性质均匀的活组织跟其他物理性质均匀的普通物质差不多,那就错得太离谱了。事实上,随便挑一种组织(无论它是皮肤组织、肌肉组织还是脑组织),用显微镜观察一下你就会发现,每种组织都由大量独立单位构成,这些小单位的性质大体上决定了组织的整体特性(图90)。这些生命体的基本结构单元通常被称为“细胞”,你也可以叫它“生物原子”(即“不可分割之物”),因为单个的细胞是保持特定组织特性的最小单位。
比如说,如果将肌肉组织切成只有半个细胞的一小块,它就会失去肌肉的收缩特性,这就像只剩半个镁原子的“金属片”也不再是镁金属,其实它已经变成了一小块碳!
构成组织的细胞尺寸很小(平均直径只有百分之一毫米)。我们熟悉的任何动植物都由极大量独立细胞组成。比如说,成年人的身体包含了几百万亿个细胞!
当然,体型较小的生物拥有的细胞数量相对也比较少;比如说,家蝇和蚂蚁体内只有几亿个细胞。单细胞生物也是一个庞大的家族,阿米巴虫、真菌(皮癣感染就是真菌引起的)和细菌都是这个家族的成员,你只有通过高倍显微镜才能看到这些只有一个细胞的小家伙。这些独立的活细胞不需要承担复杂生命体内的“社会功能”,针对它们的研究写就了生物学领域最激动人心的篇章。
要理解生命的一般特性,我们必须弄清活细胞的结构和性质。
活细胞与无生命物质,或者更确切地说,与死细胞(例如写字台里的木头细胞或者皮鞋里的皮革细胞)的区别到底是什么?
活细胞独特的基本性质包括下面几种能力:1.从周围介质中摄取自己需要的养料;2.将这些养料转化为生长发育所需的物质;3.活细胞的几何尺寸增长到一定程度以后会分成两个相似的细胞,其中每个细胞都跟自己原来的尺寸差不多,而且可以生长发育。当然,独立细胞组成的更复杂的生命体也普遍拥有这三种能力:“进食”“发育”和“繁殖”。
拥有批判性思维的读者或许会提出反对意见,因为某些无生命的物质也拥有这三种性质。举个例子,如果我们将一小块盐晶体丢进过饱和盐溶液里,它会吸收(或者说“剥离”)水中多余的盐分子。这些分子一层层堆积在晶体表面,于是晶体开始生长。我们甚至可以想象,在某些机械作用的影响下,譬如说晶体越长越大,最终它无法承受自己的重量裂成了两半,由此形成的“子晶体”又会继续生长。这样的过程怎么就不是“生命现象”呢?
2 遗传和基因
事实上,遗传学证明了我们的猜测。我们不但能证明染色体上这些名为“基因”的微型结构单元的确携带着各种各样的遗传性状,而且在很多情况下,我们还知道每段基因携带的具体遗传信息。
当然,就算是在最先进的显微镜下,所有基因看起来还是差不多,它们不同的功能深深隐藏在分子结构内部。
因此,要弄清每段基因“生命的意义”,我们只能深入研究特定动植物物种的遗传特性代代相传的方式。
3 基因,“活的分子”
层层剥开生命体的复杂结构,现在我们似乎已经触摸到了生命的基本单元。事实上,我们已经看到,隐藏在细胞深处的基因控制着生命体的整个发育过程和成熟生命体的几乎所有性状;有人或许会说,动植物的每一个个体都是“围绕”基因生长的。用物理学术语来类比的话,我们可以说基因和生命体之间的关系就像原子核和一大堆无生命的物质。从本质上说,某种物质的所有物理性质和化学性质最终都能归结到它的原子核上,而原子核的特性又由它携带的电荷数决定。比如说,携带6个基本电荷单元的原子核将吸引6个核外电子,生成的原子总是倾向于排列成规整的六边形,最终形成一种高硬度、高折射率的物质,我们称之为钻石。以此类推,一组电荷数分别为29、16和8的原子核形成的原子紧紧挤在一起,形成一种名叫硫酸铜的蓝色软晶体。当然,哪怕最简单的生命体复杂度也超过任何晶体,但无论是生命体还是晶体,它们的宏观特性都完全取决于微观的核心单元。
第四卷 宏观宇宙
第十章 不断扩展的地平线
1 地球和它的邻居
说到天文尺度的距离,我们必须先了解视差位移(简称“视差”)的概念。这个陌生的词儿听起来可能有些吓人,但事实上,视差的概念非常简单,而且十分有用。
要了解视差,我们或许可以从穿针开始。如果闭上一只眼拿线穿针,很快你就会发现这样做很难;线头要么离针鼻太远,要么太近。如果只用一只眼,你很难判断针鼻与线头之间的距离;但要是两只眼睛都睁开,你很容易将线头穿过针鼻,或者至少很容易学会。用两只眼睛观察物体的时候,你会不自觉地让两只眼睛同时聚焦在一件物体上。物体离你越近,你的眼球就向对侧转得越多,肌肉感觉到的张力会清晰地告诉你物体的距离。
2 恒星之河
我们在太空中的下一段旅程将从行星跳往恒星,视差测量法还可以继续发挥作用。但我们发现,哪怕最近的恒星离我们都太远太远,即使采用地球上相距最远的两个观察点(对跖点),我们也看不出这些星星相对于星空背景的视差位移。不过,要测量这么远的距离,我们还有别的办法。既然我们可以利用地球本身的尺寸测量地球公转轨道的大小,那又为什么不能利用公转轨道的尺寸来测量恒星的距离呢?换句话说,从地球轨道的两端观察,我们或许有可能看到至少部分恒星的相对位移。当然,这意味着我们需要等待半年才能完成两次观察,但这又有何不可呢?
……
如果恒星真的在做圆周运动,我们应该就能观察到上述现象;假如这样的运动的确存在,那么我们不仅能看到红移和蓝移,还能进一步估算恒星的公转轨道半径和运动速度。通过观察天空中明显可见的恒星运动,奥尔特看到了预想中的红移和蓝移现象,从而毫无疑义地证明了银河系的确在旋转。
通过类似的方式,我们还可以证明,银河系的旋转必将影响恒星垂直于观察者视线方向的运动速度。尽管精确测量这一速度分量非常困难(因为对于那些遥远的恒星来说,哪怕它们的线速度极大,体现在天球上的角位移也微乎其微),但奥尔特和其他天文学家的确观察到了这种效应。
如果能够精确测量恒星运动的奥尔特效应,我们就能算出恒星的公转轨道和周期。利用这个办法,我们算出太阳系绕半人马座银心旋转的轨道半径是30,000光年,也就是说,相当于整个银河系半径的2/3。太阳绕着银心转一整圈大约需要2亿年。当然,这是一段漫长的时间,不过别忘了,我们的太阳系已经50亿岁了,也就是说,它已经带着整个家族的所有行星绕着银心转了差不多20圈。参照地球年的定义,我们可以将太阳的公转周期定义为“太阳年”,以这个标准来衡量,我们的宇宙只有20岁。的确,恒星世界里的一切都发生得很慢,要描述宇宙的历史,太阳年其实是个很合适的时间单位!
3 走向未知的边界
正如我们刚才讨论的,在广袤的太空中,银河系并不是唯一的一群恒星。通过望远镜我们发现,遥远的宇宙深处还有很多类似银河系的巨型恒星团,其中最近的一个我们的裸眼甚至都能看见,它就是著名的仙女座星云。我们眼中的仙女座星云是一个模糊黯淡的长条状小星云,照片VIIA和VIIB上面显示的就是两个这样的天体群,它们分别是后发座星云的侧视图和大熊座星云的俯视图。我们注意到,就像银河系呈镜片状一样,这两个星云也拥有特殊的螺旋结构,因此我们称之为“旋涡星云”。很多迹象表明,银河系应该也是个旋涡星系,但身在其中的我们很难完全确定它的形状。事实上,我们的太阳很可能位于“银河系大星云”某条旋臂的末端。
……
现在,我们打算回答一下关于宇宙尺寸的基本问题。宇宙到底是有限的还是无限的?随着望远镜技术的不断进步,天文学家求知若渴的眼睛是否总能发现宇宙中全新的处女地?或者反过来说,我们是否应该相信,宇宙虽大,但终归有限,至少从理论上说,我们早晚会看到最后一颗新的星星?
谈到宇宙“有限”,我们当然不是说探索者可能在几十亿光年外看到一堵高墙,上面写着“禁止通行”。
事实上,在第三章中我们已经看到,空间可能是有限无界的。弯曲的空间可能形成自我封闭的结构,假设有一位太空探险家开着火箭飞船沿直线(测地线)一路往前飞,那他最后没准会回到原地。
当然,这就像某位古希腊探险家从家乡雅典出发,一路向西而行,当这段漫长的旅程结束时,他发现自己走进了雅典城东边的城门。
我们无须周游世界,只需要研究相对较小的一片区域的几何特性,就能证明地球表面是弯曲的;那么借助类似的办法,现有的望远镜足以帮助我们弄清三维宇宙空间是否弯曲。在第五章中我们已经看到,弯曲分为两种:正曲率对应的是体积有限的封闭空间,而负曲率对应的是马鞍形的开放无限空间(图42)。这两种空间的差异在于,在封闭空间中,观察者周围一定半径范围内均匀分布的物体数量增长的速度远小于半径的三次方,开放空间则与此相反。
在我们这个宇宙里,“均匀分布的物体”指的自然是独立的星系,所以要回答宇宙的曲率问题,我们只需要数数不同距离范围内的星系数量。
哈勃博士真的统计了这方面的数据,结果发现,星系数量增长的速度似乎比距离的三次方慢一些。这意味着我们的宇宙是个曲率为正的有限空间。但这里必须提到的是,哈勃观察到的这种效应非常微弱,只有在靠近威尔逊山天文台那台100英寸望远镜的视线尽头时才有一点儿征兆,近期天文学家利用帕洛马山那台新的200英寸反射式望远镜所做的观测也无助于解决这个重要问题。
目前我们仍无法准确回答宇宙是否有限的问题,还有一个原因在于,判断遥远星系的距离时,我们只能基于它们的可见亮度进行计算(遵循平方反比定律)。这种方法暗含了一个假设:所有星系的实际亮度完全相同,而且始终如一。但是如果独立星系的亮度随时间变化,也就是说,它的亮度受年龄的影响,那我们的方法可能得出谬以千里的结果。千万别忘了,天文学家通过帕洛马山望远镜看到的最遥远的星系远在10亿光年以外,现在的我们看到的实际上是它们10亿年前的状态。如果星系的亮度会随着年龄的增长而降低(这可能是因为死去的恒星越来越多,留下来的活跃恒星越来越少),那我们就必须对哈勃的结论做出修正。事实上,在10亿年(这大约相当于星系总寿命的七分之一)的时间内,星系的亮度只需要变化一个很小的百分比,就足以推翻“宇宙有限”的结论。
因此,要准确回答“宇宙是否有限”这个问题,我们还有很多工作要做。
第十一章 创世年代
1 行星的诞生
对我们这些生活在全世界七个大洲(包括南极洲伯德少将考察站)上的人来说,“坚固的大地”这个词蕴含着稳定、永久的意味。地球表面上我们熟悉的所有地貌似乎早在时间之初就已存在,无论是大陆还是海洋,山峦或者河流。事实上,根据历史地质数据,我们知道地球表面实际上一直在缓慢变化,大片的陆地可能被海洋吞没,曾经位于海底的区域也可能浮出水面。
我们还知道,老去的山脉会被雨水慢慢冲走,构造运动时时创造出新的山峰,但这一切变化都发生在我们这颗星球坚固的地壳上。
不难看出,必然存在一个坚固地壳尚未形成的时代,那时候的地球是一个岩浆组成的灼热球体。事实上,对地球内部的研究表明,这颗星球的主体至今仍处于熔化状态,我们常常在不经意间提起的“坚固大地”不过是漂浮在熔岩之上的相对较薄的一层硬壳。要证明这件事,最简单的办法莫过于测量地球内部不同深度的温度;于是我们发现,深度每增加一千米,温度就会上升30℃左右(或者说深度每增加一千英尺,温度上升16℉);比如说,在全世界最深的矿井里(南非金矿罗宾逊深井),井壁灼热滚烫,为了避免矿工们被活活烤熟,矿场不得不加装空调。
按照这样的温度增长速率,我们只需要深入地底50千米,地球的温度必然达到岩石的熔点(1200-1800℃),而这个深度还不到地球半径的百分之一。再往下走,占据了地球97%以上质量的物质必然处于完全熔化的状态。
显然,这样的状况不可能永远维持下去;实际上,刚刚诞生的地球是一个纯液态的球体,从那以后,它一直在缓慢冷却,现在的我们看到的不过是这颗星球生命历程中的一个特定阶段,而在遥远的未来,地球终有一天会完全固化。根据地球冷却的速率和硬质地壳增长的速度,我们粗略估计,这个冷却过程必然始于好几十亿年前。
……
事实上,正如我们在第九章中看到的,最简单的生命形式(例如各种病毒)实际上只是一些相当复杂的分子,它们主要由碳、氢、氧和氮原子组成。这些元素在任何新形成的行星表面都必然大量存在,所以我们必须相信,一旦硬质地壳成形,大气中的水蒸气凝聚降雨,汇成较大的水体,那么只要必需的原子按照特定顺序偶然地组合起来,地面上早晚会出现几个这样的分子。当然,由于活分子非常复杂,所以它们意外形成的概率极低,这就像你捧着装拼图的盒子晃一晃,它们又有多大的概率自动拼成完整的图案呢?不过从另一方面来说,我们千万不能忘记,不断碰撞的原子数量极多,而且它们拥有近乎无限的时间,所以生命诞生的机会并没有你想象的那么渺茫。事实上,地球的地壳形成后不久就出现了生命,这意味着初始原子可能只需要几亿年时间就能意外形成复杂的有机分子。一旦最简单的生命形式出现在新形成的行星表面上,有机繁殖过程和渐进的演化就会创造出越来越复杂的生命。我们无从得知,其他“宜居”行星上生命演化的过程是否也和地球一样。研究不同世界的生命必将为我们理解演化过程提供关键的助力。
或许在不久的将来,我们就能乘坐“核动力太空飞船”前往火星和金星探险,研究那里的生命;但是几百光年甚至几千光年外的恒星世界里是否存在生命,或者说存在什么样的生命,这或许是科学永远无法解答的谜团。
2 恒星的私生活
对恒星孕育行星的完整过程有了一个大体的了解之后,现在我们或许应该研究一下恒星本身。
恒星的一生经历了哪些事情?恒星到底是怎么诞生的,它在漫长的一生中经历过哪些变化,最终又将走向什么样的结局?
要研究恒星,我们可以从太阳入手,它是银河系亿万恒星中相当典型的一颗。首先我们知道,作为一颗恒星,太阳的寿命长得不可思议;“考古”证据表明,太阳已经以同样的亮度燃烧了几十亿年,地球上所有的生命都仰赖它的光芒。任何常规能量源都不可能持续这么长时间输出这么多能量,所以太阳辐射的来源问题一直是科学领域最令人费解的谜题之一,直到我们发现了元素的放射性嬗变和人工嬗变,隐藏在原子核深处的海量能量才开始初现端倪。在第七章中我们已经看到,几乎每一种化学元素都能充当“炼金术”燃料,每个原子内部都储藏着大量能量,如果将物质加热到几百万度,这些能量就有可能释放出来。
……
但不得不提的是,耗尽氢燃料的衰老恒星萎缩冷却的过程不一定都这么安静规矩,实际上,行将就木的恒星在生命中的“最后一英里”常常发生猛烈的爆炸,仿佛是在反抗不可改变的命运。
这些人称“新星爆发”和“超新星爆发”的壮丽事件是恒星研究领域最激动人心的课题之一。短短几天内,天空中一颗平平无奇的恒星亮度暴涨几十万倍,表面变得极度灼热。伴随着亮度的突然增加,恒星的光谱也会随之发生变化,天文学家研究了这方面的数据,结果发现,这些恒星的本体经历了急剧膨胀,外层以每秒2000千米左右的速度向外扩张。但亮度的增加只是暂时的,尺寸膨胀到了某个极限以后,恒星开始慢慢安静下来。爆炸恒星的亮度通常只需要一年左右就将恢复如初,不过在这之后很长的一段时间里,它的辐射还将出现一些比较小的变化。虽然恒星的亮度恢复了正常,但它的其他性质就不好说了。恒星的部分大气——尤其是在爆炸期间经历了急速膨胀的那一部分气体——将继续向外扩散,在恒星外部形成一层直径越来越大的发光气壳。目前我们还不清楚爆炸后恒星的性质将发生哪些永久性的变化,因为目前天文学家只拍摄到了一颗新星(御夫座新星,1918年)爆炸前的光谱照片。但就连这张照片也很不完善,无法帮助我们准确判断这颗恒星爆炸前的表面温度和直径。
通过观测所谓的超新星爆发,我们可以更好地研究恒星体爆炸造成的结果。在我们的银河系里,这样壮丽的爆炸好几个世纪才会发生一次(普通的新星爆发大约每40年就会发生一次),超新星的亮度是普通新星的几十万倍。爆发的超新星亮度峰值堪比整个星系。1572年,第谷·布拉赫(Tycho Brahe)在白天观察到的那颗星星和中国天文学家于1054年记录的另一颗星星都是银河系内超新星爆发的典型案例,伯利恒之星可能也是一颗超新星。
1885年,我们在附近的仙女座大星云里观察到了第一颗银河系外的超新星,它比以往我们观察到的银河系内的任何新星亮一千倍。尽管这样的剧烈爆炸十分罕见,但近年来我们对超新星性质的理解进展可喜,这应该归功于巴德(Baade)和兹威基(Zwicky)的观测,他们首次认识到了超新星爆发和新星爆发之间的重要区别,并开始系统性地研究出现在各个遥远星系中的超新星。
尽管超新星爆发和普通新星爆发亮度相差悬殊,但二者也有很多共同特征。二者的亮度都会急速上升,然后缓慢下降,而且它们的变化曲线形状(除了尺度以外)几乎一模一样。和普通新星一样,超新星爆发也会产生急速膨胀的气壳,不过超新星的气壳带走的质量在恒星总质量中的占比更大。事实上,新星的气壳会变得越来越薄,最终很快消散在周围的空间中;而超新星释放的大量气体会在爆炸波及的区域形成明亮的星云。比如说,1054年的那颗超新星爆发后,我们在它原来所在的位置看到了“蟹状星云”,它肯定来自恒星爆炸时喷出的气体(见照片VIII)。
蟹状星云。1054 年,中国天文学家在天空中的这片区域观察到了超新星爆发向外喷出的膨胀气体层。
我们还找到了这颗超新星爆炸后留下的残骸。事实上,我们在蟹状星云的正中央观察到了一颗黯淡的星星,根据它呈现出来的特征,我们可以确定这是一颗密度极大的白矮星。
这意味着超新星爆发的物理过程和普通新星十分相似,只是前者的规模比后者大得多。
接受新星和超新星的“坍缩理论”之前,我们先得问问自己,恒星体为什么会突然急速收缩?目前人们普遍相信的解释是,恒星实际上是灼热气体组成的大质量天体,它之所以能维持自身的形状,全靠内部灼热物质形成的高压。只要我们先前描述的恒星中央的“碳循环”过程还在继续,恒星核产生的原子能就会不断补充表面向外辐射的能量,让恒星维持原来的状态,几乎不发生任何改变。但是一旦恒星内的氢燃料耗尽,原子能彻底枯竭,恒星必然开始收缩,将自身的引力势能转化为辐射。不过,这样的引力收缩过程进行得十分缓慢,因为恒星物质热传导率极低,中心区域的热量需要很长时间才能传到表面。比如说,假如我们的太阳开始坍缩,那么至少一千万年以后,它的直径才会收缩到现在的一半。一旦超过这个收缩速率,多余的引力势能立即就会被释放出来,导致恒星内部的温度和气压上升,从而减缓收缩过程。因此我们发现,要让恒星更快地收缩,就像我们观察到的新星和超新星那样迅速坍缩,唯一的办法是设法移除收缩过程中恒星内部产生的一部分能量。比如说,如果恒星物质的热传导率提升几十亿倍,那么它的收缩速率就将增大同样的倍数,收缩的恒星将在短短几天内迅速坍缩。但是这样的可能性根本就不存在,因为现有的辐射理论清晰地表明,恒星物质的热传导率完全由恒星的密度和温度决定,要让它提升几十几百倍都很困难,更别说几十亿倍。
最近,本书作者和他的同事修罕伯格博士(Dr. Schenberg)提出,恒星坍缩的真正原因在于中微子的大量形成,我们在本书的第七章中详细讨论过这些微小的核粒子。显然,按照中微子的定义,它恰好是转移收缩恒星内部多余能量的理想介质,因为中微子能够轻而易举地穿透整个恒星体,就像窗玻璃无法阻挡普通光线一样。但我们仍不能确定,收缩恒星内部的灼热环境是否真的能够大量生成中微子。
3 原始的混沌和膨胀的宇宙
如果将宇宙当成一个整体,我们立即就会发现一个关键问题:宇宙是否会随着时间而演变?我们是否应该假设,无论过去还是未来,宇宙始终和我们现在看到的样子差不多?又或者宇宙一直都在变化,而且有不同的演化阶段?
对于这个问题,基于各学科积累的知识,我们可以做出非常明确的回答:是的,我们的宇宙一直在缓慢地变化;已被遗忘的过去、眼下的现在和遥远的将来,这三个时间点的宇宙状态各不相同。除此以外,各学科积累的丰富数据还进一步告诉我们,宇宙有一个确定的开始,从那时候起,它慢慢演化成了现在的样子。正如我们之前看到的,太阳系的年龄大约有几十亿岁,无论我们从哪个方向探查,最后算出来的数字都差不多。月球(这颗卫星显然是被太阳的强大引力从地球上撕裂出去的)也必然形成于好几十亿年前。
针对独立恒星演化过程的研究(见上一节)表明,现在我们看到的大部分恒星年龄差不多也是几十亿岁。天文学家研究了恒星的运动,尤其是双星系统、三星系统以及更复杂的星系团内部恒星的相对运动,最后得出结论:这些星星存在的时间不可能超过几十亿年。
宇宙中各种化学元素——尤其是钍和铀这类放射性元素,众所周知,它们会缓慢衰变——铀和钍的相对丰度为我们提供了另一个角度的独立证据。经历了漫长的衰变以后,如果这些元素至今仍存留在宇宙中,那么我们只能推测,要么其他更轻的原子核至今仍在不断组合形成这些重元素,要么这是最后一批年代久远的库存。
根据我们目前对核嬗变过程的认知,前一种可能性必将遭到摈弃,因为哪怕是最灼热的恒星,它的内部温度也不足以“烹制”出放射性重原子核。事实上,正如我们在上一节里看到的,恒星内部的温度大约有几千万度,但利用较轻的原子核“烹制”放射性原子核需要几十亿度的高温。
因此,我们必须假设,重原子核形成于宇宙演化过程中的某个早期阶段,在那个阶段,所有物质都处于超高温高压的可怕环境中。
……
根据化学元素丰度估算宇宙年龄的方法以核物理学为基础,由此算出的结果和天文学家观测行星、恒星和星系团得出的结论完全一致!
不过,在几十亿年前那个万物伊始的早期阶段,宇宙到底是一种什么样的状态?在后来的漫长岁月里,它又是怎样逐渐演变成了现在的样子?
要完整地解答这两个问题,我们需要深入研究“宇宙膨胀”现象。在上一章中我们已经看到,广袤的宇宙空间中充斥着无数庞大的星系(或者说恒星系),而我们的太阳不过是其中一个星系(银河系)内数十亿颗恒星之中的一颗。而且在我们能看到(当然是在200英寸望远镜的帮助下)的范围内,这些星系大体均匀分布。
通过研究遥远星系的光谱,威尔逊山天文台的天文学家E.哈勃注意到,这些星系的光谱线微微偏向红端,越遥远的星系“红移”就越明显。事实上,天文学家发现,不同星系“红移”的程度与它到地球的距离直接成正比。
要解释这种现象,最自然的想法就是假设所有星系都在离我们远去,越遥远的星系“后退”的速度越快。这个假设基于所谓的“多普勒效应”:如果光源正在靠近我们,那么光的颜色会偏向光谱的紫端;反过来说,正在远离我们的光线看起来偏红。当然,光源与观察者的相对速度必须达到一定的程度才会产生能被观察到的红移和蓝移。R.W.伍德教授(Prof. R. W. Wood)因为闯红灯被抓起来的时候就对巴尔的摩的法官提出过这个理由,他说,因为他正开车靠近红绿灯,所以他看到的灯是绿色的,这当然是狡辩。如果这位法官对物理学有一点了解,他就会要求伍德教授好好算算,要把红灯看成绿灯,他的车速需要达到多少,然后给他开张超速罚单!
回到星系“红移”的问题,乍看之下,这个现象完全不合理。宇宙中所有的星系都在逃离银河系,仿佛我们的星系里有一头大怪兽!银河系到底拥有什么可怕的特质,以至于这么不受欢迎?不过要是稍微往深里想想,你很容易就能得出结论:银河系没什么不对头,事实上,并不是其他星系对银河系敬而远之,而是所有星系都在彼此远离。请想象一个波点图案的气球(图127),当你慢慢把它吹胀,气球表面积变得越来越大,波点之间的距离也将不断增长,以任何一个点为参照,你都会觉得其他所有波点正在“逃离”它,而且在这个膨胀的气球表面,不同的点后退的速度与它和参照点之间的距离直接成正比。
通过这个例子,我们清晰地看到,哈勃之所以会观察到其他星系不断后退,并不是因为银河系的性质或者位置有何特殊之处,而只是因为,容纳所有星系的宇宙空间正在缓慢地均匀膨胀。
根据观察到的膨胀速率和相邻星系目前的距离,你可以轻松算出,这样的膨胀至少始于50亿年前。
