1均值、中位数、众数
均值mean、中位数median、众数mode
2极差、中程数
极差range、中程数mid-range
中程数是最大值和最小值的平均数。
3象形统计图
用符号表示数据类型,比如一滴血代表8个人,在统计图中画血的符号。
4条形图
bar graph
将事物进行分类,并看每一类分别的怎样的情况
5折线图
line graph
反映变化趋势
6饼图
pie graph
看各部分的占比
7误导人的折线图
8茎叶图
stem-and-leaf plot
9箱线图
box-and-whiskers plot
看数据的散布情况和中位数
先求中位数,然后以中位数为界求前后两段的中位数作为四分位数
10箱线图2
11统计:集中趋势
Statistics分为描述性统计学DescriptiveStatistics和推断统计学InferentialStatistics
Central Tendency通常用算数平均数、中位数、众数表示。
12统计:样本和总体
样本sample
总体population
样本均值$\bar x$
总体均值$\mu$
13统计:总体方差
离散程度dispersion
0 0 5 5和2 2 3 3的平均数相同
总体方差$\sigma^2=\frac{\sum_{i=1}^N(x_i-\mu)^2}{N}$
14统计:样本方差
样本方差$\sigma^2=\frac{\sum_{i=1}^n(x_i-\bar x)^2}{n}$
样本方差$\sigma^2=\frac{\sum_{i=1}^n(x_i-\bar x)^2}{n}\leq总体方差\sigma^2=\frac{\sum_{i=1}^n(x_i-\mu)^2}{n}$
总体方差的无偏估计(unbiased estimate of the population variance)或称之为无偏样本方差(unbiased sample variance)
方差$\sigma^2=\frac{\sum_{i=1}^n(x_i-\bar x)^2}{n-1}$
15统计:标准差
standard deviation标准差的单位更好
16统计:诸方差公式
总体方差$\sigma^2=\frac{\sum_{i=1}^N(x_i-\mu)^2}{N}$可化为$\sigma^2=\frac{\sum_{i=1}^Nx_i^2}{N}-\mu^2$
17随机变量介绍
random variable一般用大写字母表示,随机变量实际上是一种函数——将random process随机过程映射到实际数字的函数。如抛硬币过程:
$$X= \begin{cases} 1,&if hats\ 0,&if tails \end{cases} $$
随机变量分为连续型continuous随机变量和离散型discrete随机变量。
18概率密度函数
离散型随机变量有概率分布函数(probability distribution function)

连续型随机变量有概率密度函数(probability density function)
19二项分布1
binomial probability distribution
二项分布是n重伯努利试验成功次数的离散概率分布,X服从二项分布记作X~B(n,p),伯努利试验是只有两种可能结果的单次随机试验。
进行伯努利试验,成功(X=1)概率为p,失败(X=0)概率为1-p,随机变量X服从伯努利分布。
两点分布或称之为0-1分布
| 随机变量X | 1 | 0 |
|---|---|---|
| 概率P | p | 1-p |
20二项分布2
21二项分布3
22二项分布4
23期望值E(x)
期望值就是总体均值。
24二项分布的期望值
二项分布就是一堆两点分布。
E(x)=np
D(x)=np(1-p)
期望值就是这些经过概率加权之后的和。
25泊松过程1
Poisson Distribution泊松分布其实来自二项分布。
泊松分布适用于描述单位时间/空间内随机事件发生的次数。
泊松分布的使用场景,需要满足下面三个条件:
- 单个事件发生与否,及发生概率是独立的;
- 已知给定区间(时间/空间)内,事件平均发生次数(发生率);
- 发生的次数是有限的。
26泊松过程2
公式:假设K为给定区间内时间/空间的发生次数。参数λ为每个区间内平均发生次数 。概率可用公式表示如下:
$P(X=k)=\frac{e^{-\lambda}\lambda^k}{k!}$
推导过程需要用到第二个重要极限。

示例:一个售后服务中心,平均每周接到A项目投诉2.5次。求下周没有接到A项目的投诉的概率是多少,接到A项目投诉3次的概率是多少。

泊松分布求期望和方差非常好记,都为λ。
泊松分布求期望:
公式:如果X~po(λ),那么E(x)=λ。
示例:沿用上述A项目投诉的例子,在一周之内预计发生A项目的投诉次数为2.5次。
泊松分布求方差:
公式:如果X~po(λ),那么Var(x)=λ。
示例:沿用上述A项目投诉的例子,在一周之内预计发生A项目的投诉次数的方差为2.5次。
组合泊松分布:
公式:如果Xpo(λx),且如果Ypo(λy),则:X +Y ~ po(λx+λy)
示例:该售后服务中心,除了平均每周接到A项目的投诉2.5次,还会接到平均每周1次的B项目的投诉。下周总部会下来调查,希望收到的总投诉次数为0次,求这种情况的概率。
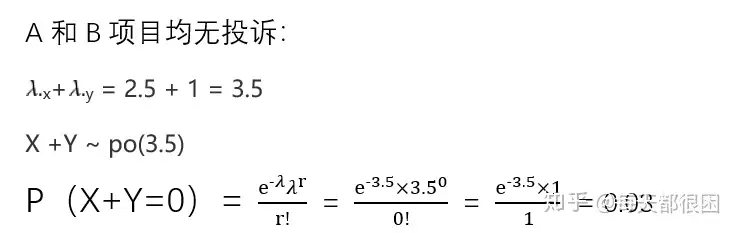
由结果可知,下周零投诉的概率为0.03。
次数过多的二项分布使用泊松分布求解:
之前在分享二项分布的时候,大家是否还记得猜箱子的小游戏?这个小游戏一共由4道题目组成,那么,假若这个小游戏有100道题目,甚至1000道题目呢?光是计算组合公式会让你算到头大。
其实在遇到这种情况时,泊松分布也可以帮上忙。那么先来回顾下二项分布的期望与方差。
二项分布的期望E(r)=np,方差Var(r)=npq,而泊松分布的期望和方差均为λ。此时我们需要这两种分布的期望和方差相近似,即np与npq近似相等的情况 。
由以上可知,当二项分布的n很大而p很小时,泊松分布可作为二项分布的近似,其中λ为np。通常当n≥20,p≤0.05时,就可以用泊松公式近似得计算。
示例:借用二项分布文章中打靶的例子,假设打靶的数量为100次,求在这100次打靶中有3次能够打中10环的概率是多少 。
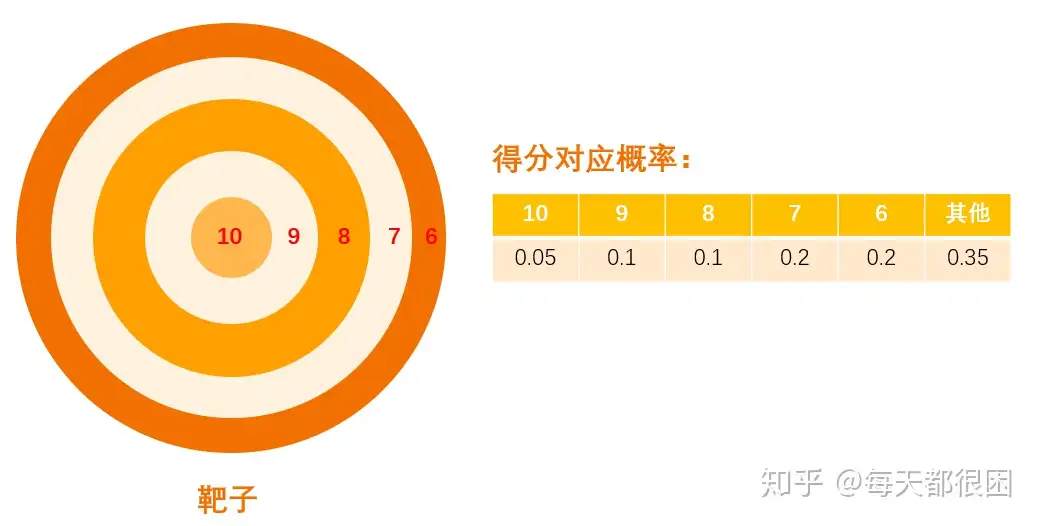
在本题中,n=100,p=0.05,np=5,使用二项分布的泊松分布近似法得到X~po(5),代入公式求出概率:
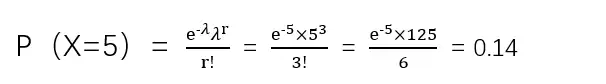
所以100次打靶中3次命中10环的概率为0.14。
27大数定律
The law of large numbers
样本量足够大时,样本均值接近期望值
赌徒谬误gambler’s fallacy:一定次数试验后,如果正面数高于均值,则大数定律会让后面的正面数更少。
大数定律不关心前面发生的情况,收敛于期望值只是因为还有无限次收敛于期望值的试验,让前面的有限次实验可以忽略。不过买彩票和赌博的人并没有遵循这个原则。赌徒们不遵循这一原则,但赌场是知道的。短期内,少量样本时,有些人能打败庄家,但长期来看,庄家肯定是赢的,因为赌局的参数是他们定的。
28正态分布Excel练习
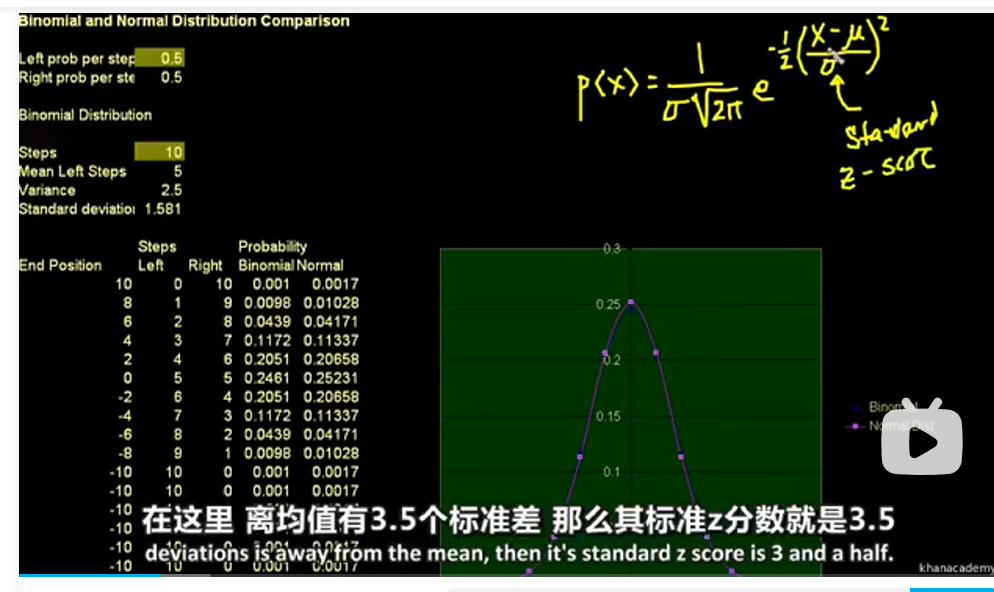
正态分布可以通过二项分布近似很好地得到。
central limit theorem中心极限定理即随机变量和的分布以正态分布为极限,即使这些试验的分布不是正态的。
29正态分布介绍
概率密度函数$p(x)=\frac{1}{\sigma \sqrt{2\pi}}exp(-\frac{(x-\mu)^2}{2\sigma^2})=\frac{1}{\sqrt{2\pi\sigma^2exp(z^2)}}$,其中标准z分数$z=\frac{x-\mu}{\sigma}$
概率就是对概率密度函数求定积分。
30正态分布问题:哪些是正态分布?
31正态分布问题:z分数
z score就是离均值有多少个标准差远
32正态分布问题:经验法则
empirical rule经验法则
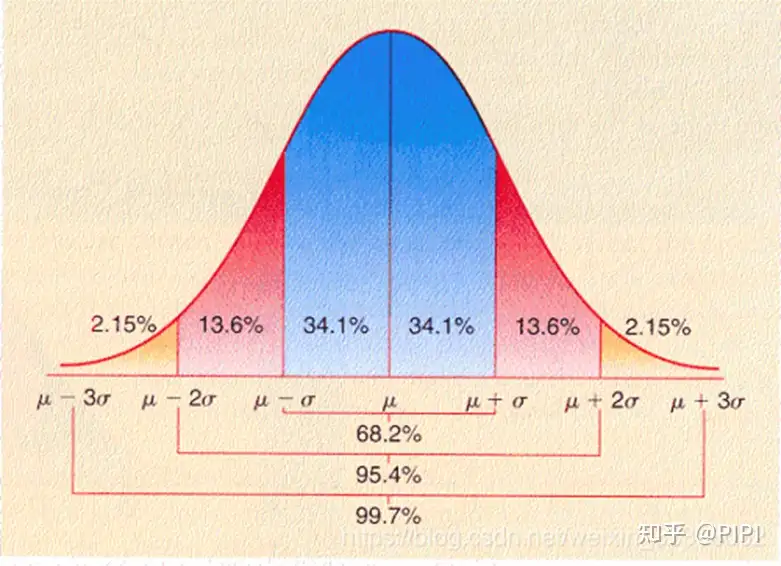
高斯分布曲线取决于两个因素,即均值和标准差。分布的均值决定了图形中心位置,标准差决定了图像的高度与宽度,标准差小时,曲线“高瘦”,标准差大时,曲线“矮胖”。
sigma原则:数值分布在(μ-σ,μ+σ)中的概率为0.6526;
2sigma原则:数值分布在(μ-2σ,μ+2σ)中的概率为0.9544;
3sigma原则:数值分布在(μ-3σ,μ+3σ)中的概率为0.9974;
基本上可以把区间(μ-3σ,μ+3σ)看作是随机变量X实际可能的取值区间,落在该区间之外的概率小于千分之三。
33练习:标准正态分布和经验法则
standard normal distribution X~N(0,1)
34经验法则和z分数的进一步练习
AP统计考试分数不是正态分布,有$\sigma和\mu$能求近似z-score。
z-score就是离均值有多少个标准差远,可以用在任何分布上,只要知道均值和标准差。
35中心极限定理
随着样本容量sample size趋于$\infty$,离散随机变量分布会趋于正态分布。
中心极限定理(central limit theorem/CLT)是概率论(probability theory)一个非常重要的结论,它指出在一定条件下,独立(independent)随机变量的标准化的(normalized)和随样本量(sample size)变大会趋向正态分布(normal distribution),即它的累积分布函数(cumulative distribution function/CDF)会收敛于标准正态分布(standard normal distribution)的CDF $N(x)=\int_{-\infty}^{x}\frac{1}{\sqrt{2\pi}}e^\frac{-x^2}{2}dx$
中心极限定理不要求随机变量本身是正态分布的,所以它带来一个非常重要的结果:在一定条件下,我们可以使用对正态分布成立的方法去应对非正态分布。比如,对于样本量 � 足够大时,二项分布(binomial distribution)$Bin(n,p)$ 可以用正态分布$N(np, np(1-p))$ 来近似。用具体事例来表达,如果我们抛 500 次硬币,由于每次抛硬币正面朝上的概率为 12 ,我们可以将正面朝上的数量近似地视作一个 $N(250,125)$ 的随机变量。中心极限定理有很多种版本,也有对于非独立变量的变式。在本篇文章中,我们将要介绍对于独立变量的中心极限定理的三个版本。有经典中心极限定理、林德伯格中心极限定理、李雅普诺夫中心极限定理、多维中心极限定理几种。
36样本均值的抽样分布
Online Statistics Education: An Interactive Multimedia Course of Study
sampling distribution of the sample mean
完美正态分布的偏度skew是0。如果偏度为正,意味着右侧尾部较长,即均值向左偏。
峰度kurtosis
正峰度——高
偏度
偏度(Skewness)可以用来度量随机变量概率分布的不对称性。
公式:
$S=\frac{1}{n}\sum_{i=1}^n [(\frac{X_i-\mu}{\sigma})^3]$
其中 $\mu$ 是均值, $\sigma$是标准差。
计算例子:
一组数据为1、2、2、4、1,均值为2,标准差约为1.22,所以偏度为
$S=15×[(1−21.22)^3+(2−21.22)^3+…+(1−21.22)^3]≈1.36$
几何意义:
偏度的取值范围为(-∞,+∞)
当偏度<0时,概率分布图左偏。
当偏度=0时,表示数据相对均匀的分布在平均值两侧,不一定是绝对的对称分布。
当偏度>0时,概率分布图右偏。
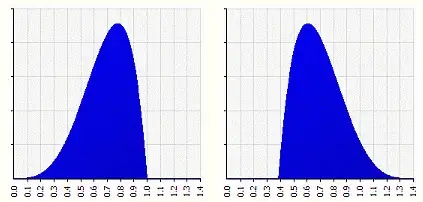
例如上图中,两个概率分布图都是均值=0.6923,标准差=0.1685的,但是他们的形状是不一样的,左图偏度=-0.537,形状左偏,右图偏度=0.537,形状右偏。
峰度
峰度(Kurtosis)可以用来度量随机变量概率分布的陡峭程度。
公式:
$K=\frac{1}{n}\sum_{i=1}^n [(\frac{X_i-\mu}{\sigma})^4]$
其中 $\mu$ 是均值, $\sigma$是标准差。
几何意义:
峰度的取值范围为[1,+∞),完全服从正态分布的数据的峰度值为 3,峰度值越大,概率分布图越高尖,峰度值越小,越矮胖。
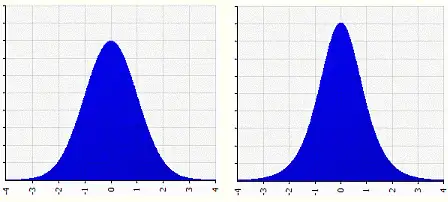
例如上图中,左图是标准正态分布,峰度=3,右图的峰度=4,可以看到右图比左图更高尖。
通常我们将峰度值减去3,也被称为超值峰度(Excess Kurtosis),这样正态分布的峰度值等于0,当峰度值>0,则表示该数据分布与正态分布相比较为高尖,当峰度值<0,则表示该数据分布与正态分布相比较为矮胖。
37样本均值的抽样分布2
随着样本容量增大,分布会怎么变化?
当$n->\infty$时样本均值的抽样分布变为正态分布。一般来说,n=10或15就已经很接近正态分布了。
38均值标准误差
标准差standard deviation也被称为标准偏差,是描述各数据偏离平均数的距离的平均数,表征的是数据的离散程度。
标准误差Standard error表征的是单个统计量在多次抽样中呈现出的变异性。
前者表示数据本身的变异性,后者表征的是抽样行为的变异性。
随着样本容量的增大,会发生两件事:一是更接近正态分布,二是标准差更小。
样本均值抽样分布的方差等于原分布的方差除以n即$\sigma^2_{\bar x}=\frac{\sigma^2}{n}$
标准误差等于原分布标准差除以根号n即$\sigma_{\bar x}=\frac{\sigma}{\sqrt n}$
39抽样分布例题
The average male drinks 2L of water when active outdoors (with a standard deviation of .7L). You are planning a full day nature trip for 50 men and will bring 110L of water. What is the probability that you will run out?
P(run out) = P(usr more than 110L) = P(average water use per man is > 2.2L/m)
Sampling distribution of the sample mean when n=50
$\mu_{\bar x}=\mu=2L$
$\sigma_{\bar x}=\frac{\sigma}{\sqrt n}=\frac{0.7}{\sqrt 50}=0.099$
$z-score=\frac{X-\mu}{\sigma_{\bar x}}=\frac{2.2-2}{0.099}=2.02$
水不够的概率即是样本均值大于均值右侧2.020个标准差处的概率,根据z表格来求低于某值的概率。
P($\bar x$ will be more than 2.022 standard deviation above the mean)=1-0.9783=0.0217=2.17%
40置信区间
e.g. You sample 36 apples from your farm’s harvest of over 200,000 apples. The mean weight of the sample is 112grams(with a 40 gram sample standard deviation). What is the probability that the mean weight of all 200,000 apples is within 100 and 124 grams?
即求总体均值落在样本均值左右12g范围内的概率。
P($\mu$ is within 12 of $\bar X$)=P($\bar X$ is within 12 of $\mu$)
重新写成这样之后,我们就会自然想到使用样本均值抽样分布。
P($\bar X$ is within 12 of $\mu$)=P($\bar X$ is within 12 of $\mu_{\bar x}$)
即求某一特定样本均值落在抽样分布均值左右12g范围内的概率。
$\sigma_{\bar x}=\frac{\sigma}{\sqrt n}=\frac{40}{\sqrt 36}=6.67$
$z-score=\frac{X-\mu}{\sigma_{\bar x}}=\frac{12}{6.67}=1.8$
根据z表格来求低于1.8个标准差的概率为0.9641。(这里只能从右边计算)
所求概率$P=2*(0.9641-0.5)=0.9282$
41伯努利分布均值和方差的例子
伯努利分布是两点分布。
离散分布期望值是各种可能值概率加权后的和。
| 支持与否 | 不支持0 | 支持1 |
|---|---|---|
| 概率 | 0.4 | 0.6 |
期望值=0.6
方差=$0.4*(0-0.6)^2+0.6*(1-0.6)^2=0.4*0.6=0.24$
42伯努利分布均值和方差的公式
$\mu = p$
$\sigma^2 = (1-p)(0-p)^2+p(1-p)^2=p(1-p)$
43误差范围1
随机调查100人的投票意愿,选B的(认为是事件1)有43人,选A的(认为是事件0)有57人。样本均值为0.43,方差为0.2475,样本标准差0.50,标准误差0.05。
找到这样一个合理置信区间,95%确信总体真实均值p值落在其中的区间
样本均值、抽样分布均值、总体均值是统计学中的重要概念,它们之间的区别如下:
样本均值:是指从总体中随机抽取一个样本,并计算该样本中所有观测值的平均数。样本均值是对样本数据的一个统计描述,通常用作总体均值的估计值。
抽样分布均值:是指从总体中抽取多个样本,并计算所有样本均值的平均数。抽样分布均值是对样本均值的分布的一个描述,它的均值通常等于总体均值。
总体均值:是指总体中所有观测值的平均数。总体均值是一个未知参数,通常需要通过样本统计量来估计。
总体均值是一个固定的未知参数,而样本均值和抽样分布均值是随机变量,它们的取值会随着不同的样本选择而变化。在统计学中,通过样本均值来估计总体均值是一种常见的方法,而抽样分布均值则用于评估样本均值的变异情况。
44误差范围2
找出一个合理的置信区间,95%的几率确信总体真实均值$\mu=p=\mu_{\bar x}$落在其中的区间
在正态分布中,样本均值落在两个标准差范围内的概率是95.44%。
抽样分布的均值等于原分布的均值。抽样分布标准差是标准误差,不是样本标准差。
误差范围margin of error是另一种描述置信区间confidence interval的方式。
- P($\bar X$ is within $2\sigma_{\bar x}$ of $\mu_{\bar X}$)=95.4%
- P(p is within $2\sigma_{\bar x}$ of $\bar X$)=95.4%
- P(p is with 2(0.05) of $\bar X$)=95%(从这里开始往下都是约等号)
- P(p is with 2(0.05) of $\bar X$)=95%
- P(p is with 0.1 of $\bar X$)=95%
- P(p is within 0.33~0.53)=95%
45置信区间例题
从6250名教师中随机抽取250人询问他们是否认为计算机是教室必备教学工具。其中,142名教师认为是必备的教学工具(记为事件1),108名教师认为不是必备的教学工具(记为事件0)。
| \|X=1 | X=0 | |
|---|---|---|
| P | 0.568 | 0.432 |
均值为0.568,方差为0.246,样本标准差为0.496四舍五入为0.50,抽样分布标准差(标准误差)近似于样本标准差除以根号下样本容量,$\sigma_{\bar x}$=0.031
注:用p(1-p)计算得到的方差为0.245
1.Calculate a 99% confidence interval for the proportion of teachers who felt that computers are an essential teaching tool.
$0.99/2=0.495$
$0.495+0.5=0.995$
查询z-table发现0.995对应的数值为2.58,即有大概99%的概率使得样本均值落在抽样分布均值左右2.58个标准差(对应的概率为99.02%)范围内。抽样分布均值也就是原分布的均值,也就是认为计算机必备的老师占比p。这个值未知,但它有一个不错的估计值。
我们有99%的把握认为样本均值0.568落在概率p左右0.08范围内,也即有99%的把握认为概率p落在0.568左右0.08范围内。
置信区间为0.488~0.648,我们相信有99%几率真实概率p在这里两个数字之间。
2.How could the survey be changed to narrow the confidence interval but to maintain the 99% confidence interval?
保持99%置信水平的前提下如何缩小置信区间?抽取更大样本即可。
置信区间是指对于一个总体参数(比如总体均值或总体比例),基于样本数据,计算出的一个区间,使得该区间内包含该总体参数真实值的概率达到预先设定的置信水平。换句话说,置信区间是对总体参数真实值的一个估计,它告诉我们该估计的可靠程度。例如,假设我们想要估计某个产品的平均销售量。我们可以从该产品的销售记录中随机抽取一些样本,计算出样本均值和样本标准差。然后,我们可以使用样本均值和样本标准差,基于正态分布理论,计算出一个置信区间。例如,如果我们设置置信水平为95%,那么该置信区间将会包含95%的情况下真实的总体均值。这个区间的端点称为置信下限和置信上限。置信区间的宽度取决于样本大小、置信水平和总体标准差等因素。置信水平越高,置信区间就越宽;样本容量越大,置信区间就越窄;总体标准差越小,置信区间就越窄。置信区间是统计推断的重要工具,它可以帮助我们对总体参数的真实值做出合理的推断和决策。
样本容量越大,抽样分布标准差就越小,置信区间通常就越窄。
这是因为样本容量的增加会减小样本均值和总体均值之间的差异,从而使得置信区间变窄。具体而言,当样本容量增加时,样本均值的方差会减小,因此样本均值周围的误差也会减小,这就会导致置信区间的宽度减小。同时,当样本容量增加时,抽样分布的形状会趋近于正态分布,这也会使得置信区间变窄。需要注意的是,当总体标准差或置信水平固定时,样本容量越大,置信区间就越窄。但是,如果置信水平随样本容量的增加而提高,那么置信区间的变化可能会更加复杂。此外,当总体标准差未知时,使用样本标准差来计算置信区间时,样本容量的增加会使得样本标准差和抽样分布的自由度变化,这也需要考虑到。因此,总体标准差、置信水平、样本容量等因素的变化都会对置信区间的宽度产生影响,需要在实际问题中具体分析和判断。
46小样本容量置信区间
样本容量<30通常被认为是糟糕的估计。
7个病人服药后血压分别上升了1.5, 2.9, 0.9, 3.9, 3.2, 2.1和1.9。Construct a 95% confidence interval for the true expected blood pressure increase for all patients in a population.
均值为2.34,标准差为1.04,$\sigma_{\bar x}$=0.39
这个视频里要讲的是,我们关注抽样分布,以此来生成区间。这里抽样分布不能像原来那样认为是正态分布使用中心极限定理之类的。我们需要改变抽样分布,不再假设是正态分布。我们假设是所谓的t分布。可以认为t分布是专门为更好估计小容量样本的置信区间所设计的。
t分布是一种概率分布,通常用于在样本容量较小的情况下进行总体参数的推断。t分布由英国统计学家威廉·塞奇威克(William Sealy Gosset)于西元1908年提出,因此也被称为“塞奇威克t分布”。t分布的形状类似于正态分布,但是相比于正态分布,它的峰度较低,而且尾部较厚。这是因为t分布的概率密度函数是基于样本标准差来计算的,而样本标准差本身是一个不稳定的估计量,其方差会随着样本容量的减小而增加。因此,在样本容量较小的情况下,t分布的形状会更加扁平和宽,以保证在总体均值未知时,对样本均值的推断更加准确。t分布的参数是自由度(degrees of freedom,df),自由度是指用于计算样本标准差的样本数量减去1。自由度越大,t分布就越接近于正态分布。在实践中,t分布通常用于构建置信区间或进行假设检验,以便对总体参数进行推断。
计算t分布的置信区间通常需要以下步骤:
确定置信水平(confidence level)和自由度(degrees of freedom,df)。通常情况下,置信水平取值为95%或99%,自由度的计算方法取决于具体的问题,例如在单样本t检验中,自由度为n-1,其中n为样本容量。
计算样本均值(sample mean)和样本标准差(sample standard deviation)。样本均值是指样本中所有观测值的平均数,样本标准差是指样本中所有观测值与样本均值的差的平方和的平均数的平方根。
计算t值(t statistic)。t值是指样本均值与总体均值之间的差异除以标准误差(standard error)的比值,其中标准误差是指样本标准差除以样本容量的平方根。t值的计算公式为:
t = (sample mean - population mean) / (sample standard deviation / sqrt(sample size))
其中,sample mean为样本均值,population mean为总体均值,sample standard deviation为样本标准差,sample size为样本容量。
根据置信水平和自由度,查找t分布表(或使用计算机软件)得到t临界值(t critical value)。
计算置信区间。置信区间可以通过以下公式计算:
confidence interval = sample mean ± t临界值 × (sample standard deviation / sqrt(sample size))
其中,sample mean为样本均值,t临界值为根据置信水平和自由度从t分布表或计算机软件中查找得到的t值,sample standard deviation为样本标准差,sample size为样本容量。
通过以上步骤,可以得到t分布的置信区间,该区间表示总体参数的真实值有一定的概率落在该区间内。需要注意的是,计算t分布的置信区间时,需要满足一些假设条件,例如样本来自正态分布总体或样本容量较大等,否则计算结果可能不可靠。
置信水平为95%,自由度为6,查询t表格(该分布关于中轴对称,所以叫双侧。单侧表示一直到特定值的累积百分比。本题是对称的,用two-sided。)此时对应两侧2.447个标准差。t表格中说的标准差是通过样本标准差得到的估计值。
$\sigma_{\bar x}$=0.39,$\sigma_{\bar x}\times 2.447=0.96$,置信区间为1.38~3.30
说置信区间是因为这都是估计值。
47假设检验和p值
假设检验需要两个假设,一个是原假设(null hypothesis),另一个是备择假设(alternative hypothesis)。
原假设是一个被假定的基准假设,通常表示研究者想要测试的“无效”或“无差异”的情况。在进行假设检验时,我们会假定原假设为真,并通过数据来判断是否拒绝原假设。
备择假设则是对原假设的补充或对立假设,通常表示研究者想要证明的“有效”或“有差异”的情况。如果拒绝原假设,则可以接受备择假设。
因此,假设检验需要两个假设来进行比较和决策。通过比较数据与原假设的符合程度,我们可以判断是否有足够的证据来拒绝原假设,从而接受备择假设。
p值是指在假设检验中,根据样本数据计算出的一个概率值,表示在原假设为真的情况下,出现观测结果或更极端结果的概率。p值越小,代表观测到的数据与原假设不一致的可能性越大。
p值的主要作用是帮助我们做出关于原假设是否应被拒绝的决策。通常,我们会预先设定一个显著性水平(significance level)作为决策的标准,一般为0.05或0.01。如果计算出的p值小于显著性水平,则拒绝原假设,认为观测到的数据与原假设不一致;反之,则接受原假设。
除了用于决策的作用,p值还可以提供一些定量的信息。例如,p值越小,代表观测到的数据与原假设的差异越明显,可能性越小;而p值越大,则表示观测到的数据与原假设的差异越小,可能性越大。
需要注意的是,p值只能提供关于原假设是否应被拒绝的决策和一些定量信息,而不能确定原假设是否真实或备择假设是否正确。因此,在解释p值时,需要结合具体的实际背景和领域知识,进行综合分析。
例:已知没有注射药物的老鼠平均反应时间是1.2秒,100只注射药物的老鼠的平均反应时间为1.05秒,样本标准差为0.5秒。药物对反应时间有影响吗?
这里我们需要建立两个假设。
第一个假设是原假设(null hypothesis) H0: 药物对反应时间没影响
第二个假设是备择建设(alternative hypothesis)H:药物对反应时间有影响
假设Ho为真,然后求样本均值1.05,标准差0.5这一结果的概率,如果这个概率特别小,则认为原假设为假。
抽样分布均值=总体均值
抽样分布标准差等于总体标准差除以根号下样本容量,而总体标准差近似于样本标准差。
z-score = 3
根据经验法则,均值左右3个标准差内的概率为99.7%。
得到样本均值1.05,标准差0.5这一结果甚至更极端结果的概率为0.3%,这个概率特别小,因此我们认为原假设为假。
很多论文中,得到零假设中这种极端情况甚至更极端情况的概率称为p值。本题中p值为0.003。
48单侧检验和双侧检验
单侧检验和双侧检验是假设检验中常用的两种检验方式。
单侧检验(one-tailed test)是指在假设检验中,备择假设只包含一个方向的偏差,例如只考虑检验均值是否大于某个特定值,或者只考虑检验均值是否小于某个特定值。单侧检验所关心的只是一个方向的差异,因此在计算p值时,只需要考虑备择假设的一个方向即可。
双侧检验(two-tailed test)是指在假设检验中,备择假设包含两个方向的偏差,例如考虑检验均值是否与某个特定值不同,即既可能大于特定值,也可能小于特定值。双侧检验所关心的是两个方向的差异,因此在计算p值时,需要将备择假设的两个方向都考虑进去。
在进行单侧检验或双侧检验时,需要根据具体的实际背景和研究问题来确定使用哪种检验方式。如果研究者只关心一个方向的差异,可以选择单侧检验;如果研究者关心两个方向的差异,需要选择双侧检验。此外,在进行假设检验时,还需要注意选择适当的显著性水平和合适的假设检验方法,以得到准确、可靠的结果。
上题中我们只能说药物有一定效果,用药后的均值同原均值不一样,但没说增加还是减少了反应时间。
检验是否存在效果,这是双侧检验。
检验是否能减少平均反应时间,这是单侧检验。if H0, P(result lowers than 1.05s)=0.0015
49z统计量VSt统计量
$z统计量=\frac{\bar X -\mu_{\bar X}}{\frac{\sigma}{\sqrt n}} =\frac{\bar X -\mu_{\bar X}}{\frac{S}{\sqrt n}}$(正态分布、样本容量>30)
$t统计量=\frac{\bar X -\mu_{\bar X}}{\frac{S}{\sqrt n}}$(t分布、样本容量小)
50 第一型错误
第一型错误(Type I error)是指在假设检验中,拒绝了原假设,但实际上原假设是正确的,也就是错误地认为存在某种差异或效应。第一型错误通常用α表示,也称为显著性水平。
在假设检验中,我们需要设定一个显著性水平,通常为0.05或0.01,作为决策的标准。如果计算出的p值小于显著性水平,我们会拒绝原假设,认为观测到的数据与原假设不一致,也就是存在某种差异或效应。但如果实际上原假设是正确的,那么我们就会犯第一型错误,错误地认为存在差异或效应。
第一型错误是假设检验中一个比较严重的错误,因为它会导致我们得出错误的结论,浪费研究资源,也可能对决策产生严重后果。因此,在进行假设检验时,需要设定适当的显著性水平,并根据具体实际情况进行综合分析,以减少第一型错误的概率。
第一型错误和第二型错误是假设检验中两种不同类型的错误。
第一型错误(Type I error)是指拒绝原假设,但实际上原假设是正确的,也就是错误地认为存在某种差异或效应。第一型错误的概率通常用α表示,也称为显著性水平。
第二型错误(Type II error)是指接受原假设,但实际上原假设是错误的,也就是错误地认为不存在某种差异或效应。第二型错误的概率通常用β表示。
可以看出,第一型错误和第二型错误的区别在于错误的方向不同。第一型错误是错误地拒绝了原假设,而第二型错误是错误地接受了原假设。
在假设检验中,我们需要设定一个显著性水平作为决策的标准,以判断是否拒绝原假设。但在实际应用中,往往存在着一定的风险和成本,例如错失某种重要的差异或效应,或者浪费研究资源。因此,在进行假设检验时,需要综合考虑第一型错误和第二型错误,并选择适当的显著性水平和样本大小,以尽可能降低两种错误的概率。
在假设检验中,设定显著性水平是做出决策的关键因素之一。通常,显著性水平设定为0.05或0.01,这表示在原假设为真的情况下,出现观测结果或更极端结果的概率不超过5%或1%。显著性水平越小,代表拒绝原假设的标准越高,对差异或效应的要求也越高,但可能会导致第二型错误的概率增加。
设定显著性水平时,需要考虑具体的实际背景和研究问题,以及假设检验的目的和要求。如果研究对象是生命、财产等重大事项,或决策后果十分严重,需要设定更高的显著性水平,以尽可能降低第一型错误的概率;如果研究对象是对差异或效应的要求不高,或者样本量比较大,可以适当降低显著性水平,以降低第二型错误的概率。
此外,还需要考虑假设检验的类型和样本大小等因素。例如,在单侧检验中,显著性水平需要分配给备择假设的一个方向;在样本量较小的情况下,需要设定更高的显著性水平,以尽可能避免漏诊。
总之,设定显著性水平需要综合考虑各种因素,并根据具体情况进行灵活调整,以得到准确、可靠的假设检验结果。
51小样本假设检验
例题:The mean emission of all engines of a new design needs to be below 20 ppm if the design is to meet new emission requirements. Ten engines are manufactured for testing purposes, and the emission level of each is determined. The emission data is :
15.6 16.2 22.5 20.5 16.4 19.4 16.6 17.9 12.7 13.9
Does tje data supply sufficient evidence to conclude that this type of engine meets the new standard? Assume we are willing to risk a Type I error with probability = 0.01
均值=17.17标准差为2.98
H0:不满足标准$\mu=20ppm$
H1:满足标准即实际均值低于20ppm($\mu< 20ppm$
先认为原假设H0成立,如果样本均值得到17.17的概率小于1%,我们就拒绝原假设
$t=\frac{17.17-20}{\frac{2.98}{\sqrt 10}}=-3.00$
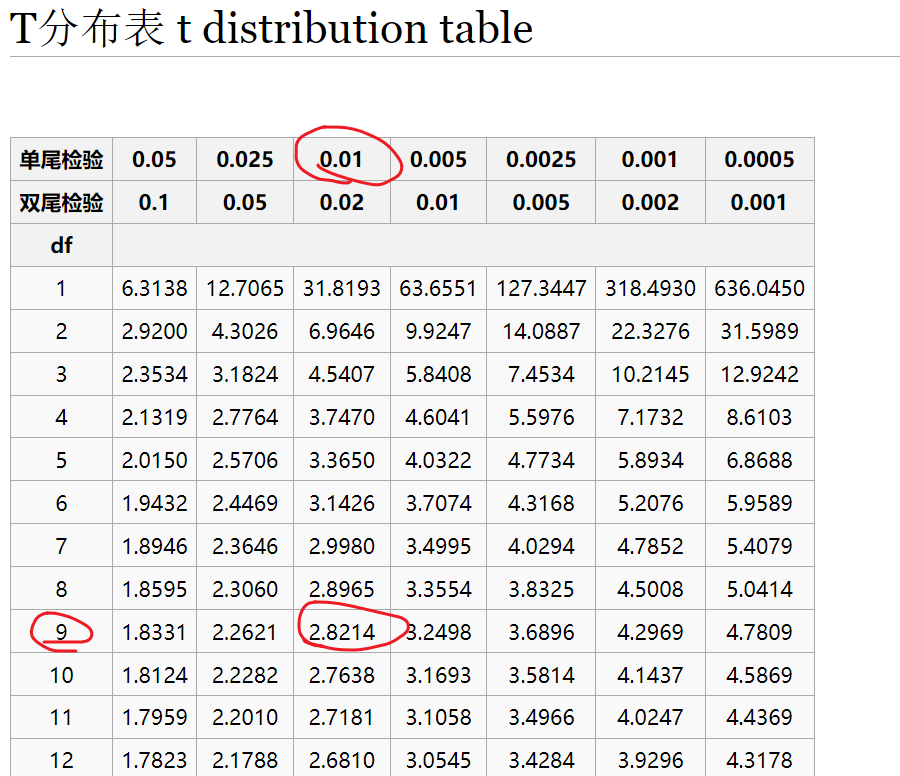
由对称性,查表知单侧t临界值为-2.8214,即t值小于-2.8214的概率是1%。我们算出的t值是-3.00,这显然进入了让我们拒绝原假设的区域,t值得到-3.00的概率比1%还小,所以我们可以相对可靠地拒绝原假设,接受备择假设即满足排放标准。而且这里犯第一型错误的概率低于1%。
52t统计量置信区间
计算t分布的置信区间通常需要以下步骤:
确定置信水平(confidence level)和自由度(degrees of freedom,df)。通常情况下,置信水平取值为95%或99%,自由度的计算方法取决于具体的问题,例如在单样本t检验中,自由度为n-1,其中n为样本容量。
计算样本均值(sample mean)和样本标准差(sample standard deviation)。样本均值是指样本中所有观测值的平均数,样本标准差是指样本中所有观测值与样本均值的差的平方和的平均数的平方根。
计算t值(t statistic)。t值是指样本均值与总体均值之间的差异除以标准误差(standard error)的比值,其中标准误差是指样本标准差除以样本容量的平方根。t值的计算公式为:
t = (sample mean - population mean) / (sample standard deviation / sqrt(sample size))
其中,sample mean为样本均值,population mean为总体均值,sample standard deviation为样本标准差,sample size为样本容量。
根据置信水平和自由度,查找t分布表(或使用计算机软件)得到t临界值(t critical value)。
计算置信区间。置信区间可以通过以下公式计算:
confidence interval = sample mean ± t临界值 × (sample standard deviation / sqrt(sample size))
其中,sample mean为样本均值,t临界值为根据置信水平和自由度从t分布表或计算机软件中查找得到的t值,sample standard deviation为样本标准差,sample size为样本容量。
通过以上步骤,可以得到t分布的置信区间,该区间表示总体参数的真实值有一定的概率落在该区间内。需要注意的是,计算t分布的置信区间时,需要满足一些假设条件,例如样本来自正态分布总体或样本容量较大等,否则计算结果可能不可靠。
t分布通常在样本容量较小的情况下使用。这是因为在小样本情况下,往往我们无法准确知道总体的标准差,所以我们使用样本标准差代替,这就引入了更多的不确定性,t分布就是在这种情况下用来估计未知总体均值的一种方法。但是,尽管t分布常常用于小样本量的情况,但也不是说在大样本量的情况下就不能使用。实际上,当样本量增大时,t分布会逐渐接近正态分布。所以,如果样本量较大,使用t分布和正态分布的结果差异通常很小,可以视为可忽略不计。另外,正如你所提到的,使用t分布需要满足一些前提假设,其中一个重要的假设是样本来自正态分布的总体。如果这个假设不满足,t分布可能就不是一个好的选择。
总的来说,t分布是一个在特定情况下使用的工具,其适用性取决于样本大小、样本来源等因素。
置信水平为95%,自由度为9,查询t表格(该分布关于中轴对称,所以叫双侧。单侧表示一直到特定值的累积百分比。本题是对称的,用two-sided。)此时对应两侧2.262个标准差。t表格中说的标准差是通过样本标准差得到的估计值。
$\sigma_{\bar x}$=17.17,$\sigma_{\bar x}\times 2.262=2.13$,置信区间为15.04~19.30
说置信区间是因为这都是估计值。
53大样本占比假设检验
例:We want to test the hypothesis that more than 30% of U.S. households have Internet access( with a significance level of 5%). We collect a sample of 150 households and find that 57 access.
要进行假设检验,首先要设定零假设和备择建设。零假设也就是要检验的内容不正确,这里零假设是美国家庭总体的互联网接入率小于等于30%。备择假设和要检验的一致即接入率大于30%。
然后我们要根据零假设得到一个总体中的占比值p,在这个假设下,看样本中150户中57户接入互联网的概率是多少?如果该概率小于5%,小于我们的显著性水平,那么我们就能拒绝零假设,接受备择假设。
一开始假设零假设是正确的,根据该假设,我们得到总体均值$\mu$或者说总体占比p,伯努利分布中$\mu=p$。我要选择的这个占比值需要尽可能让得到这种情况的概率最大。得到样本中这种情况的概率现在还不知道。样本占比0.38,总体占比为0.3。
根据伯努利分布,总体标准差$\sigma_{H_0}=\sqrt{(0.3)\times(0.7)}=\sqrt{0.21}$
根据二项分布,np>5,n(1-p)>5
样本占比分布的标准差$\sigma_{\bar P}=\frac{\sigma_{H_0}}{\sqrt{150}}=0.037$
$zscore=\frac{\bar P - \mu_{\bar P}}{\sigma_{\bar P}}=2.14$
我们关心的单侧分布得到这个z统计量的概率是多于还是少于5%,如果少于5%,我们将拒绝零假设,接受备择假设。
根据z-table,zscore对应的概率为0.9834,1-0.9834<0.05,拒绝零假设,接受备择假设。
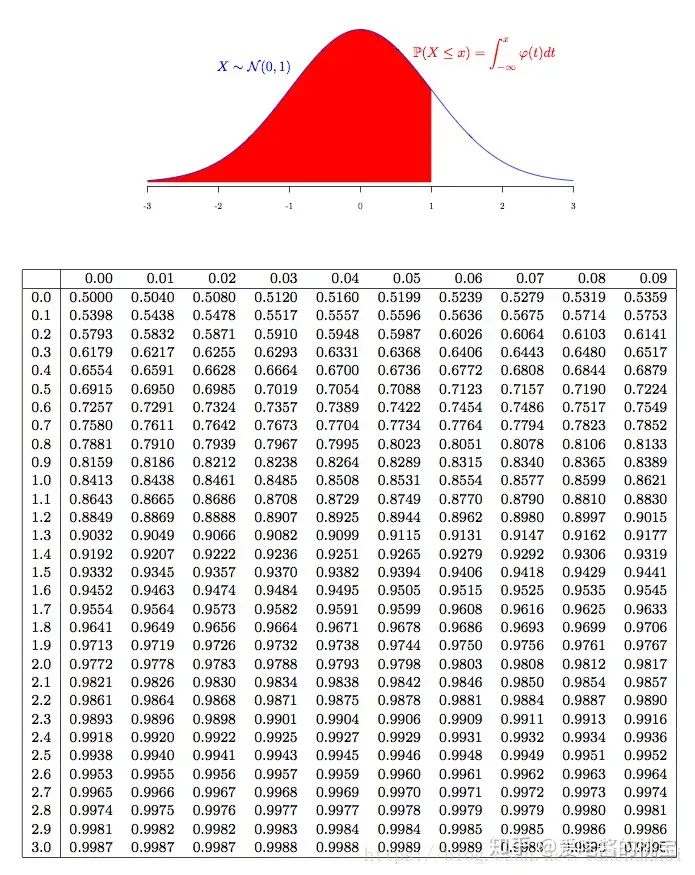
54随机变量之差的方差
independent random variables X,Y
$E(x)=\mu_x$
$Var(x)=E((X-\mu_x)^2)=\sigma_x^2$ X的方差等于X离其均值距离平方的期望值
Z=X+Y==>E(Z)=E(X)+E(Y)
Var(Z)=Var(X)+Var(Y)
Z=X-Y==>E(Z)=E(X)-E(Y)
Var(Z)=Var(X)+Var(-Y)=Var(X)+Var(Y)
$E(a \times X+b)=aE(X)+b$
$D(a \times X+b)=a^2D(X)$
两个独立随机变量之差的方差等于两个方差之和
55样本均值之差的分布
Z=X-Y==>E(Z)=E(X)-E(Y)
Var(Z)=Var(X)+Var(-Y)=Var(X)+Var(Y)
样本均值抽样分布的方差$\sigma_{\bar x}^2=\frac{\sigma_x^2}{n}$
$\sigma_x^2$为实际总体分布的方差,而不是样本均值抽样分布的方差
$\sigma_{\bar y}^2=\frac{\sigma_y^2}{m}$
$\sigma_{\bar x- \bar y}^2=\sigma_{\bar x}^2+\sigma_{\bar y}^2=\frac{\sigma_x^2}{n}+\frac{\sigma_y^2}{m}$
56均值之差的置信区间
例:We’re trying to test whether a new, low-fat diet actually helps obese people lose weight. 100 randomly assigned obese people are assigned to group 1 and put on the low fat diet. Another 100 randomly assigned obese people assigned to group 2 and put on a diet of approximately the same amount of food, but not as low in fat. After 4 months, the mean weight loss was 9.31 lbs. for group 1 (s=4.67) and 7.40 lbs.(s=4.04) for group 2.
low -fat group : ${\bar X_1}=9.31,s_1=4.67$
control group: ${\bar X_2}=7.40, s_2=4.04$
${\bar X_1}-{\bar X_2}=1.91$
$\sigma_{\bar x- \bar y}=\sqrt{\sigma_{\bar x}^2+\sigma_{\bar y}^2}=\sqrt{\frac{\sigma_x^2}{n}+\frac{\sigma_y^2}{m}}=\sqrt{\frac{s_1^2}{100}+\frac{s_2^2}{100}}=0.617$
95%置信区间
z-score对应的概率为97.5%
查阅z-table得到临界z值为1.96
有95%几率分布的实际均值落在1.91左右1.96个标准差内即置信区间为0.70~3.12
这里并非真正有95%几率实际均值的实际差值落在这个范围内,我们只是相信有95%的几率样本均值之差的实际期望值(实际均值的实际差值)落在0.7到3.12范围内,因为总体标准差或方差并非已知值。
这个置信区间其实也是总体期望值之差的置信区间。如果给所有可能的人第一种节食方式,给所有可能的人第二种节食方式,这将给出总体均值之差的置信区间。根据这个结果,也许第一种节食方式是有效的,因为即使是置信区间的下限处仍然比第二种节食方式减轻更多体重。
57均值之差的置信区间的澄清
$\mu_{\bar X - \bar Y}=\mu_{\bar X_1}-\mu_{\bar X_2}=\mu_1-\mu_2$
$\mu_1-\mu_2$是低脂节食同非低脂节食减肥效果的真实差异值,95%置信区间中,低脂节食方式更具减肥效果。
58均值之差的假设检验
零假设:减肥效果无差异即$\mu_1-\mu_2=0$
备择假设:(单侧)第一种节食方式减肥效果更好即$\mu_1-\mu_2>0$
5%显著性水平是说拒绝正确零假设的几率只有5%,也就是犯第一型错误的概率是5%。如果得到的概率小于5%,我们就拒绝原假设。
首先假设有一个标准化正态分布,这样才能求出临界z值,
根据z-table,95%对应的z值是1.65
$\sigma_{\bar x- \bar y}=\sqrt{\sigma_{\bar x}^2+\sigma_{\bar y}^2}=\sqrt{\frac{\sigma_x^2}{n}+\frac{\sigma_y^2}{m}}=\sqrt{\frac{s_1^2}{100}+\frac{s_2^2}{100}}=0.617$
如果第一种节食方式没效果的话,两个样本均值之差超过1.02的概率只有5%,但实际我们得到的均值的差值是1.91,这显然落在临界值之外,零假设前提下,得到这个的概率小于5%,得到这个差值的概率比显著性水平要低,我们拒绝零假设,接受备择假设即低脂节食方式确实能帮助减去更多体重。
59总体占比的比较1
讨论男女投票情况是否有差异。找一个$\bar P_1-\bar P_2$ 的95%置信区间
1000men 642 -1 rest -0 $\bar P_1=0.642$
sampling distribution of $\bar P_1$
$\sigma_{\bar P_1}^2=\frac{\sigma_{P_1^2}}{n}=\frac{P_1(1-P_1)}{1000}$
1000 women 591 -1 rest -0 $\bar P_2=0.591$
sampling distribution of $\bar P_2$
$\sigma_{\bar P_2}^2=\frac{\sigma_{P_2^2}}{n}=\frac{P_2(1-P_2)}{1000}$
$\sigma_{\bar P_1- \bar P_2}=\sqrt{\frac{P_1(1-P_1)}{1000}+\frac{P_2(1-P_2)}{1000}}=0.022$
60总体占比的比较2
$\bar P_1- \bar P_2=0.051$
conf: 95% chance that $\bar P_1- \bar P_2$ is within d(distance) of 0.051 也即 95%几率 0.051在均值$\bar P_1- \bar P_2$周围d之内

95%的几率对应表中的97.5%,对应的zscore是1.96
$d=1.96\sigma_{\bar P_1- \bar P_2}=0.043$
有95%的几率总体占比之差在样本占比之差左右0.043范围内
投给某一特定候选人的男女总体占比之差的95%置信区间为[0.008, 0.094]
该范围男性比女性占比更大
61总体占比比较的假设检验
检验投给某个候选人的男性占比同女性占比之间是否有显著不同
零假设是不存在差异,即$P_1- P_2=0$,P=0.6165
显著性水平定为5%,双侧检验,均值左侧和均值右侧很远处的极端情况,都将让我们拒绝零假设。zscore对应的累积概率是97.5%。
备择假设是存在差异。
$\sigma_{\bar P_1- \bar P_2}=\sqrt{\frac{2P(1-P)}{1000}}=0.0217$
$zscore=\frac{\bar P_1-\bar P_2-(P_1-P_2)}{\sigma_{\bar P_1- \bar P_2}}=2.34$
只有5%几率,零假设前提下,从z统计量中抽取的样本值大于1.96。
拒绝零假设,选择备择假设。
62线性回归中的平方误差
$y=mx+b$
$SE_{line}=(y_1-mx_1-b)^2+…+(y_n-mx_n-b)^2$
找m, b使得平方误差和SE最小
63线性回归公式的推导1
对上面的公式进行展开 $SE_{line}=(y_1^2+y_2^2+…+y_n^2)-2m(x_1y_1+x_2y_2+…+x_ny_n)-2b(y_1+y_2+…+y_n)+m^2(x_1^2+x_2^2+…+x_n^2+2mb(x_1+x_2+…+x_n)+nb^2$
64线性回归公式的推导2
n个点同直线之间平方误差之和
$SE_{line}=n{\bar {y^2}}-2mn\bar {xy}-2bn \bar y+m^2n{\bar {x^2}}+2mbn\bar x+nb^2$
65线性回归公式的推导3
最小化需要对m,b分别求偏导然后令两个式子等于0计算出对应的m,b
最小值点位于对m和b的斜率都为0的位置
$\frac{\partial SE_{line}}{m}=-2n\bar {xy}+2nm{\bar {x^2}}+2bn{\bar {x}}=0$
$\frac{\partial SE_{line}}{b}=-2n{\bar {y}}+2mn{\bar {x}}+2bn=0$
推导出$m{\bar {x}}+b={\bar {y}}$
$m\frac{{\bar {x^2}}}{{\bar {x}}}+b=\frac{{\bar {xy}}}{\bar {x}}$
可以发现两点都在直线上
66线性回归公式的推导4
上面得到的结果消元求解
$m=\frac{{\bar {x}{\bar {y}}-{\bar {xy}}}}{({\bar {x}})^2-{\bar {x^2}}}$
$b={\bar {y}}-m{\bar {x}}$
67线性回归例题
3个点(1,2)、(2,1),(4,3)
$m=\frac{7}{3}$
$b=1$
68决定系数R2
total variation in y: $SE_y = (y_1-\bar y)^2+(y_2-\bar y)^2+…+(y_n-\bar y)^2$
没被描述的波动$SE_{line}$,这个值越小,说明拟合效果越好
总波动种被直线描述的百分比即决定系数coefficient of determination,记作R2=$1-\frac{SE_{line}}{SE_{y}}$
69线性回归例题2
70计算R2
71协方差和回归线
两个随机变量之间的协方差covariance定义:两个随机变量离各自均值距离之积的期望值
$Cov(X,Y)=E[(X-E(X))(Y-E(Y))]=E(XY)-E[XE(Y)]-E(E(X)Y]+E[E(X)E(Y)]=E(XY)-E(X)E(Y)$
协方差近似表示$Cov(XY)={\bar {xy}}-{\bar {x}}{\bar {y}}$
$Var(X)=Cov(X,X)={\bar {x^2}}-({\bar {x}})^2$
$m=\frac{Cov(X,Y)}{Var(X)}$
72 $\chi^2分布$
卡方分布(英语:chi-square distribution, χ²-distribution,或写作χ²分布)是概率论与统计学中常用的一种概率分布。k个独立的标准正态分布变量的平方和服从自由度为k的卡方分布。卡方分布是一种特殊的伽玛分布,是统计推论中应用最为广泛的概率分布之一,例如假说检定和置信区间的计算。
由卡方分布延伸出来皮尔森卡方检定常用于:
1.样本某性质的比例分布与母体理论分布的拟合优度(例如某行政机关男女比是否符合该机关所在城镇的男女比);
2.同一母体的两个随机变量是否独立(例如人的身高与交通违规的关联性);
3.二或多个母体同一属性的同质性检定(义大利面店和寿司店的营业额有没有差距)。(详见皮尔森卡方检定)
概率密度函数
累积分布函数
χ^2(卡方)分布是一种概率分布,通常用于统计学中的假设检验和置信区间构建。它可以用于比较观察值和期望值之间的差异,如在卡方检验中使用。在实际应用中,χ^2分布通常用于分析分类数据的差异和相关性。
χ^2分布的形状取决于自由度参数,自由度是一个与样本大小和数据维度有关的参数。当自由度越大时,χ^2分布趋向于正态分布,并且具有更小的方差。χ^2分布的平均值等于自由度,方差等于两倍自由度。
在假设检验中,可以将观察值与期望值之间的差异表示为χ^2统计量,然后将该统计量与χ^2分布进行比较,以判断观察值是否符合期望值。如果χ^2统计量的值很大,那么观察值与期望值之间的差异就很大,表明可能存在某种关系或者模型不适合该数据。
当我们想要测试一个硬币是否是公平的时候,我们可以进行一项硬币投掷实验。我们将硬币投掷n次,然后记录正面朝上的次数x。如果硬币是公平的,则我们期望正面朝上的次数为n/2。我们可以使用χ^2分布来判断观察值x是否符合期望值n/2。
具体地,我们可以计算出χ^2统计量:
χ^2 = Σ (observed - expected)^2 / expected
其中,observed是观察到的正面朝上的次数,expected是期望正面朝上的次数,即n/2。
假设我们将硬币投掷了10次,观察到正面朝上的次数为4。此时,期望正面朝上的次数为10/2=5。我们可以计算出χ^2统计量:
χ^2 = (4-5)^2/5 + (6-5)^2/5 = 0.2
接下来,我们可以使用χ^2分布表或者软件来查找自由度为1的χ^2分布,自由度为1表示我们只有一个自由度参数,即n-1=10-1=9。根据分布表或者软件,我们可以得到χ^2分布在自由度为1时的临界值为3.84。因为计算出的χ^2统计量0.2小于临界值3.84,所以我们不能拒绝原假设,即该硬币是公平的。
这个例子说明了如何使用χ^2分布来进行假设检验。如果χ^2统计量大于临界值,则我们可以拒绝原假设,即观察值不符合期望值,可能存在某种关系或者模型不适合该数据。
卡方分布表
p-value = 1- p_CDF.
χ2越大,p-value越小,则可信度越高。通常用p=0.05作为阈值,即95%的可信度。
常用的χ2与p-value表如下:
| 自由度k \ P value (概率) | 0.95 | 0.90 | 0.80 | 0.70 | 0.50 | 0.30 | 0.20 | 0.10 | 0.05 | 0.01 | 0.001 |
| 1 | 0.004 | 0.02 | 0.06 | 0.15 | 0.46 | 1.07 | 1.64 | 2.71 | 3.84 | 6.64 | 10.83 |
| 2 | 0.10 | 0.21 | 0.45 | 0.71 | 1.39 | 2.41 | 3.22 | 4.60 | 5.99 | 9.21 | 13.82 |
| 3 | 0.35 | 0.58 | 1.01 | 1.42 | 2.37 | 3.66 | 4.64 | 6.25 | 7.82 | 11.34 | 16.27 |
| 4 | 0.71 | 1.06 | 1.65 | 2.20 | 3.36 | 4.88 | 5.99 | 7.78 | 9.49 | 13.28 | 18.47 |
| 5 | 1.14 | 1.61 | 2.34 | 3.00 | 4.35 | 6.06 | 7.29 | 9.24 | 11.07 | 15.09 | 20.52 |
| 6 | 1.63 | 2.20 | 3.07 | 3.83 | 5.35 | 7.23 | 8.56 | 10.64 | 12.59 | 16.81 | 22.46 |
| 7 | 2.17 | 2.83 | 3.82 | 4.67 | 6.35 | 8.38 | 9.80 | 12.02 | 14.07 | 18.48 | 24.32 |
| 8 | 2.73 | 3.49 | 4.59 | 5.53 | 7.34 | 9.52 | 11.03 | 13.36 | 15.51 | 20.09 | 26.12 |
| 9 | 3.32 | 4.17 | 5.38 | 6.39 | 8.34 | 10.66 | 12.24 | 14.68 | 16.92 | 21.67 | 27.88 |
| 10 | 3.94 | 4.86 | 6.18 | 7.27 | 9.34 | 11.78 | 13.44 | 15.99 | 18.31 | 23.21 | 29.59 |
73 皮尔逊$\chi^2$检验
例题:检验给出的分布和观测的数据是否吻合
| Day | M | T | W | W | F | S |
|---|---|---|---|---|---|---|
| Expected% | 10 | 10 | 15 | 20 | 30 | 15 |
| Observed | 30 | 14 | 34 | 45 | 57 | 20 |
H0:给出的分布正确
H1:给出的分布不正确
显著性水平定为5%,如果$\chi ^2$统计量得到如此极端甚至更极端的概率大于显著性水平则接受H0
观测到的人数总和为200,根据分布,得到下面的期望值
| Day | M | T | W | W | F | S |
|---|---|---|---|---|---|---|
| Expected% | 10 | 10 | 15 | 20 | 30 | 15 |
| Observed | 30 | 14 | 34 | 45 | 57 | 20 |
| Expected | 20 | 20 | 30 | 40 | 60 | 30 |
具体地,我们可以计算出χ^2统计量:
χ^2 = Σ (observed - expected)^2 / expected=11.44
自由度=6-1=5(知道5条就能得知第6条)
临界$\chi^2$统计量为11.07<11.44
拒绝原假设H0
显著性水平(significance level)是用于衡量统计推断中错误地拒绝原假设的概率。通常情况下,显著性水平被预先设定为一个小于1的数值,通常是0.05或0.01。这个数值表示如果原假设是真的,我们错误地拒绝原假设的概率,也就是犯第一类错误的概率。
但是,显著性水平并不能代表原假设的正确率。原假设的正确率是指原假设为真时,我们正确地接受原假设的概率。这个概率通常称为“功效”(power),并且取决于多种因素,包括样本大小、效应大小、显著性水平和统计方法等。
因此,在进行统计推断时,我们需要同时考虑显著性水平和功效,以便全面评估统计推断结果的可靠性和准确性。我们希望显著性水平尽可能小,以减少犯第一类错误的概率,但同时也需要考虑功效,以确保我们可以检测到真实的效应。
74 列联表$\chi^2$检验
contingency table列联表
| \ | Herb1 | Herb2 | Placebo安慰剂 | 患病或不患病的总人数 |
|---|---|---|---|---|
| sick | 30 | 30 | 30 | 80(21%) |
| not sick | 100 | 110 | 90 | 300(79%) |
| 服用各种类型物品的总人数 | 120 | 140 | 120 | 380 |
| 预计患病人数 | 25.3 | 29.4 | 25.3 | |
| 预计没患病人数 | 94.7 | 110.6 | 94.7 |
H0:草药无效果
H1:有效果
显著性水平10%
$\chi^2=\frac{(20-25.3)^2}{25.3}+\frac{(30-29.4)^2}{29.4}+\frac{(20-25.3)^2}{25.3}+\frac{(100-94.7)^2}{94.7}+\frac{(110-110.6)^2}{110.6}+\frac{(100-94.7)^2}{94.7}=2.53$
列联表自由度=(行数-1)(列数-1)
本题自由度为2
4.60>2.53
根据现有数据,我们接受原假设。我们不能确定药草是否无效,但我们也不能说药草有效,我们无法拒绝原假设。虽然这不是100%正确,但我们无法拒绝它。
75方差分析1:计算总平方和
| C1 | C2 | C3 |
|---|---|---|
| 3 | 5 | 5 |
| 2 | 3 | 6 |
| 1 | 4 | 7 |
总平均值为4
总平方和$SST=(3-4)^2+(2-4)^2+(1-4)^2+(5-4)^2+(5-4)^2+(4-4)^2+(5-4)^2+(6-4)^2+(7-4)^2=30$ 自由度是数据数-1,因为知道了总均值,最后一个值可以计算出来。
这里自由度为$3\times3-1=9-1=8$
76方差分析2:组内和组间平方和
$\bar x_1=2,\bar x_2=4,\bar x_3=6$
组内平方和SSW:各点同各自组均值的距离平方之和
$SSW=(3-2)^2+(2-2)^2+(1-2)^2+(5-4)^2+(5-4)^2+(4-4)^2+(5-6)^2+(6-6)^2+(7-6)^2=6$
每组已知均值,每组n个数据,自由度为n-1
这里自由度$3\times(3-1)=6$
总波动中有这么多来自组内波动。
组间平方和SSB:来自均值之间的波动
$SSB=3\times(2-4)^2+3\times(4-4)^2+3\times(6-4)^2=24$
一般而言,如果有m组,m个均值,自由度为m-1。
这里自由度为3-1=2
$SST=SSW+SSB$
总自由度=m-1+m(n-1)=mn-1
77方差分析3:F统计量假设检验
F检定 (F-test),亦称联合假设检定(joint hypotheses test)、变异数比率检验、方差齐性检验。它是一种在零假设(null hypothesis, H0)之下,统计值服从F-分布的检验。其通常是用来分析用了超过一个参数的统计模型,以判断该模型中的全部或一部分参数是否适合用来估计母体。
F检验这名称是由美国数学家兼统计学家George W. Snedecor命名,为了纪念英国统计学家兼生物学家罗纳德·费雪(Ronald Aylmer Fisher)。Fisher在1920年代发明了这个检验和F-分布,最初称为变异数比率(Variance Ratio)。
适用场合
检定一系列服从正态分布的母体是否有相同的标准差,此为最典型的F检定,此检定亦应用于变异数分析(ANOVA)中。
回归分析
- 检定整条回归模型是否具有解释力,此即Overall F检定 (Overall F test) 。
- 检定回归模型中特定自变数是否具有解释力,即偏回归系数是否为零,此即偏F检定(Partial F test)。
注意事项
F检验对于数据的正态性非常敏感,因此在进行变异数同质性(homoscedasticity)检定时,Levene检验, Bartlett检验或者Brown–Forsythe检验的稳健性都要优于F检验。 F检验还可以用于三组或者多组之间的均值比较,但是如果被检验的数据无法满足均是正态分布的条件时,该数据的稳健型会大打折扣,特别是当显著性水平比较低时。但是,如果数据符合正态分布,而且alpha值至少为0.05,该检验的稳健型还是相当可靠的。
若两个母体有相同的方差(方差齐性),那么可以采用F检验,但是该检验会呈现极端的非稳健性和非常态性,可以用t检验、巴特勒特检验等取代。
与其它统计值的关系
- F检验的分子、分母其实各是一个卡方变数除以各自的自由度。
- F检定用以检定单一变数可否排除于模型外时,即进行只缩减单一变数之偏F检定(Partial F test)时,$F=t^{2}$。 可参见 线性回归偏回归系数β的t检验。
这里存在一个无法衡量的总体均值,我们想知道是否有总体均值1=总体均值2=总体均值3?
H0:三组食物影响无差异
H1:有差异
显著性水平定为10%,临界F值是3.46(右尾检验,分子自由度为2,分母自由度为6)
Assume H0:
$F-statistic=\frac{\frac{SSB}{m-1}}{\frac{SSW}{m(n-1)}}$即组间平方和除以其自由度然后除以组内平方和除以其自由度
本题中F统计量为12
F分布其实是两个$\chi^2$分布之比
The F distribution is a right-skewed distribution used most commonly in Analysis of Variance. When referencing the F distribution, the numerator degrees of freedom are always given first, as switching the order of degrees of freedom changes the distribution (e.g., F(10,12) does not equal F(12,10) ). For the four F tables below, the rows represent denominator degrees of freedom and the columns represent numerator degrees of freedom. The right tail area is given in the name of the table. For example, to determine the .05 critical value for an F distribution with 10 and 12 degrees of freedom, look in the 10 column (numerator) and 12 row (denominator) of the F Table for alpha=.05. F(.05, 10, 12) = 2.7534. You can use the interactive F-Distribution Applet to obtain more accurate measures.
F Table for α = 0.10

| \|分子df1=1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 12 | 15 | 20 | 24 | 30 | 40 | 60 | 120 | ∞ | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 分母df2=1 | 39.86346 | 49.50000 | 53.59324 | 55.83296 | 57.24008 | 58.20442 | 58.90595 | 59.43898 | 59.85759 | 60.19498 | 60.70521 | 61.22034 | 61.74029 | 62.00205 | 62.26497 | 62.52905 | 62.79428 | 63.06064 | 63.32812 |
| 2 | 8.52632 | 9.00000 | 9.16179 | 9.24342 | 9.29263 | 9.32553 | 9.34908 | 9.36677 | 9.38054 | 9.39157 | 9.40813 | 9.42471 | 9.44131 | 9.44962 | 9.45793 | 9.46624 | 9.47456 | 9.48289 | 9.49122 |
| 3 | 5.53832 | 5.46238 | 5.39077 | 5.34264 | 5.30916 | 5.28473 | 5.26619 | 5.25167 | 5.24000 | 5.23041 | 5.21562 | 5.20031 | 5.18448 | 5.17636 | 5.16811 | 5.15972 | 5.15119 | 5.14251 | 5.13370 |
| 4 | 4.54477 | 4.32456 | 4.19086 | 4.10725 | 4.05058 | 4.00975 | 3.97897 | 3.95494 | 3.93567 | 3.91988 | 3.89553 | 3.87036 | 3.84434 | 3.83099 | 3.81742 | 3.80361 | 3.78957 | 3.77527 | 3.76073 |
| 5 | 4.06042 | 3.77972 | 3.61948 | 3.52020 | 3.45298 | 3.40451 | 3.36790 | 3.33928 | 3.31628 | 3.29740 | 3.26824 | 3.23801 | 3.20665 | 3.19052 | 3.17408 | 3.15732 | 3.14023 | 3.12279 | 3.10500 |
| 6 | 3.77595 | 3.46330 | 3.28876 | 3.18076 | 3.10751 | 3.05455 | 3.01446 | 2.98304 | 2.95774 | 2.93693 | 2.90472 | 2.87122 | 2.83634 | 2.81834 | 2.79996 | 2.78117 | 2.76195 | 2.74229 | 2.72216 |
| 7 | 3.58943 | 3.25744 | 3.07407 | 2.96053 | 2.88334 | 2.82739 | 2.78493 | 2.75158 | 2.72468 | 2.70251 | 2.66811 | 2.63223 | 2.59473 | 2.57533 | 2.55546 | 2.53510 | 2.51422 | 2.49279 | 2.47079 |
| 8 | 3.45792 | 3.11312 | 2.92380 | 2.80643 | 2.72645 | 2.66833 | 2.62413 | 2.58935 | 2.56124 | 2.53804 | 2.50196 | 2.46422 | 2.42464 | 2.40410 | 2.38302 | 2.36136 | 2.33910 | 2.31618 | 2.29257 |
| 9 | 3.36030 | 3.00645 | 2.81286 | 2.69268 | 2.61061 | 2.55086 | 2.50531 | 2.46941 | 2.44034 | 2.41632 | 2.37888 | 2.33962 | 2.29832 | 2.27683 | 2.25472 | 2.23196 | 2.20849 | 2.18427 | 2.15923 |
| 10 | 3.28502 | 2.92447 | 2.72767 | 2.60534 | 2.52164 | 2.46058 | 2.41397 | 2.37715 | 2.34731 | 2.32260 | 2.28405 | 2.24351 | 2.20074 | 2.17843 | 2.15543 | 2.13169 | 2.10716 | 2.08176 | 2.05542 |
| 11 | 3.22520 | 2.85951 | 2.66023 | 2.53619 | 2.45118 | 2.38907 | 2.34157 | 2.30400 | 2.27350 | 2.24823 | 2.20873 | 2.16709 | 2.12305 | 2.10001 | 2.07621 | 2.05161 | 2.02612 | 1.99965 | 1.97211 |
| 12 | 3.17655 | 2.80680 | 2.60552 | 2.48010 | 2.39402 | 2.33102 | 2.28278 | 2.24457 | 2.21352 | 2.18776 | 2.14744 | 2.10485 | 2.05968 | 2.03599 | 2.01149 | 1.98610 | 1.95973 | 1.93228 | 1.90361 |
| 13 | 3.13621 | 2.76317 | 2.56027 | 2.43371 | 2.34672 | 2.28298 | 2.23410 | 2.19535 | 2.16382 | 2.13763 | 2.09659 | 2.05316 | 2.00698 | 1.98272 | 1.95757 | 1.93147 | 1.90429 | 1.87591 | 1.84620 |
| 14 | 3.10221 | 2.72647 | 2.52222 | 2.39469 | 2.30694 | 2.24256 | 2.19313 | 2.15390 | 2.12195 | 2.09540 | 2.05371 | 2.00953 | 1.96245 | 1.93766 | 1.91193 | 1.88516 | 1.85723 | 1.82800 | 1.79728 |
| 15 | 3.07319 | 2.69517 | 2.48979 | 2.36143 | 2.27302 | 2.20808 | 2.15818 | 2.11853 | 2.08621 | 2.05932 | 2.01707 | 1.97222 | 1.92431 | 1.89904 | 1.87277 | 1.84539 | 1.81676 | 1.78672 | 1.75505 |
| 16 | 3.04811 | 2.66817 | 2.46181 | 2.33274 | 2.24376 | 2.17833 | 2.12800 | 2.08798 | 2.05533 | 2.02815 | 1.98539 | 1.93992 | 1.89127 | 1.86556 | 1.83879 | 1.81084 | 1.78156 | 1.75075 | 1.71817 |
| 17 | 3.02623 | 2.64464 | 2.43743 | 2.30775 | 2.21825 | 2.15239 | 2.10169 | 2.06134 | 2.02839 | 2.00094 | 1.95772 | 1.91169 | 1.86236 | 1.83624 | 1.80901 | 1.78053 | 1.75063 | 1.71909 | 1.68564 |
| 18 | 3.00698 | 2.62395 | 2.41601 | 2.28577 | 2.19583 | 2.12958 | 2.07854 | 2.03789 | 2.00467 | 1.97698 | 1.93334 | 1.88681 | 1.83685 | 1.81035 | 1.78269 | 1.75371 | 1.72322 | 1.69099 | 1.65671 |
| 19 | 2.98990 | 2.60561 | 2.39702 | 2.26630 | 2.17596 | 2.10936 | 2.05802 | 2.01710 | 1.98364 | 1.95573 | 1.91170 | 1.86471 | 1.81416 | 1.78731 | 1.75924 | 1.72979 | 1.69876 | 1.66587 | 1.63077 |
| 20 | 2.97465 | 2.58925 | 2.38009 | 2.24893 | 2.15823 | 2.09132 | 2.03970 | 1.99853 | 1.96485 | 1.93674 | 1.89236 | 1.84494 | 1.79384 | 1.76667 | 1.73822 | 1.70833 | 1.67678 | 1.64326 | 1.60738 |
| 21 | 2.96096 | 2.57457 | 2.36489 | 2.23334 | 2.14231 | 2.07512 | 2.02325 | 1.98186 | 1.94797 | 1.91967 | 1.87497 | 1.82715 | 1.77555 | 1.74807 | 1.71927 | 1.68896 | 1.65691 | 1.62278 | 1.58615 |
| 22 | 2.94858 | 2.56131 | 2.35117 | 2.21927 | 2.12794 | 2.06050 | 2.00840 | 1.96680 | 1.93273 | 1.90425 | 1.85925 | 1.81106 | 1.75899 | 1.73122 | 1.70208 | 1.67138 | 1.63885 | 1.60415 | 1.56678 |
| 23 | 2.93736 | 2.54929 | 2.33873 | 2.20651 | 2.11491 | 2.04723 | 1.99492 | 1.95312 | 1.91888 | 1.89025 | 1.84497 | 1.79643 | 1.74392 | 1.71588 | 1.68643 | 1.65535 | 1.62237 | 1.58711 | 1.54903 |
| 24 | 2.92712 | 2.53833 | 2.32739 | 2.19488 | 2.10303 | 2.03513 | 1.98263 | 1.94066 | 1.90625 | 1.87748 | 1.83194 | 1.78308 | 1.73015 | 1.70185 | 1.67210 | 1.64067 | 1.60726 | 1.57146 | 1.53270 |
| 25 | 2.91774 | 2.52831 | 2.31702 | 2.18424 | 2.09216 | 2.02406 | 1.97138 | 1.92925 | 1.89469 | 1.86578 | 1.82000 | 1.77083 | 1.71752 | 1.68898 | 1.65895 | 1.62718 | 1.59335 | 1.55703 | 1.51760 |
| 26 | 2.90913 | 2.51910 | 2.30749 | 2.17447 | 2.08218 | 2.01389 | 1.96104 | 1.91876 | 1.88407 | 1.85503 | 1.80902 | 1.75957 | 1.70589 | 1.67712 | 1.64682 | 1.61472 | 1.58050 | 1.54368 | 1.50360 |
| 27 | 2.90119 | 2.51061 | 2.29871 | 2.16546 | 2.07298 | 2.00452 | 1.95151 | 1.90909 | 1.87427 | 1.84511 | 1.79889 | 1.74917 | 1.69514 | 1.66616 | 1.63560 | 1.60320 | 1.56859 | 1.53129 | 1.49057 |
| 28 | 2.89385 | 2.50276 | 2.29060 | 2.15714 | 2.06447 | 1.99585 | 1.94270 | 1.90014 | 1.86520 | 1.83593 | 1.78951 | 1.73954 | 1.68519 | 1.65600 | 1.62519 | 1.59250 | 1.55753 | 1.51976 | 1.47841 |
| 29 | 2.88703 | 2.49548 | 2.28307 | 2.14941 | 2.05658 | 1.98781 | 1.93452 | 1.89184 | 1.85679 | 1.82741 | 1.78081 | 1.73060 | 1.67593 | 1.64655 | 1.61551 | 1.58253 | 1.54721 | 1.50899 | 1.46704 |
| 30 | 2.88069 | 2.48872 | 2.27607 | 2.14223 | 2.04925 | 1.98033 | 1.92692 | 1.88412 | 1.84896 | 1.81949 | 1.77270 | 1.72227 | 1.66731 | 1.63774 | 1.60648 | 1.57323 | 1.53757 | 1.49891 | 1.45636 |
| 40 | 2.83535 | 2.44037 | 2.22609 | 2.09095 | 1.99682 | 1.92688 | 1.87252 | 1.82886 | 1.79290 | 1.76269 | 1.71456 | 1.66241 | 1.60515 | 1.57411 | 1.54108 | 1.50562 | 1.46716 | 1.42476 | 1.37691 |
| 60 | 2.79107 | 2.39325 | 2.17741 | 2.04099 | 1.94571 | 1.87472 | 1.81939 | 1.77483 | 1.73802 | 1.70701 | 1.65743 | 1.60337 | 1.54349 | 1.51072 | 1.47554 | 1.43734 | 1.39520 | 1.34757 | 1.29146 |
| 120 | 2.74781 | 2.34734 | 2.12999 | 1.99230 | 1.89587 | 1.82381 | 1.76748 | 1.72196 | 1.68425 | 1.65238 | 1.60120 | 1.54500 | 1.48207 | 1.44723 | 1.40938 | 1.36760 | 1.32034 | 1.26457 | 1.19256 |
| ∞ | 2.70554 | 2.30259 | 2.08380 | 1.94486 | 1.84727 | 1.77411 | 1.71672 | 1.67020 | 1.63152 | 1.59872 | 1.54578 | 1.48714 | 1.42060 | 1.38318 | 1.34187 | 1.29513 | 1.23995 | 1.16860 | 1.00000 |
F Table for α = 0.01
| \|df1=1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 12 | 15 | 20 | 24 | 30 | 40 | 60 | 120 | ∞ | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| df2=1 | 4052.181 | 4999.500 | 5403.352 | 5624.583 | 5763.650 | 5858.986 | 5928.356 | 5981.070 | 6022.473 | 6055.847 | 6106.321 | 6157.285 | 6208.730 | 6234.631 | 6260.649 | 6286.782 | 6313.030 | 6339.391 | 6365.864 |
| 2 | 98.503 | 99.000 | 99.166 | 99.249 | 99.299 | 99.333 | 99.356 | 99.374 | 99.388 | 99.399 | 99.416 | 99.433 | 99.449 | 99.458 | 99.466 | 99.474 | 99.482 | 99.491 | 99.499 |
| 3 | 34.116 | 30.817 | 29.457 | 28.710 | 28.237 | 27.911 | 27.672 | 27.489 | 27.345 | 27.229 | 27.052 | 26.872 | 26.690 | 26.598 | 26.505 | 26.411 | 26.316 | 26.221 | 26.125 |
| 4 | 21.198 | 18.000 | 16.694 | 15.977 | 15.522 | 15.207 | 14.976 | 14.799 | 14.659 | 14.546 | 14.374 | 14.198 | 14.020 | 13.929 | 13.838 | 13.745 | 13.652 | 13.558 | 13.463 |
| 5 | 16.258 | 13.274 | 12.060 | 11.392 | 10.967 | 10.672 | 10.456 | 10.289 | 10.158 | 10.051 | 9.888 | 9.722 | 9.553 | 9.466 | 9.379 | 9.291 | 9.202 | 9.112 | 9.020 |
| 6 | 13.745 | 10.925 | 9.780 | 9.148 | 8.746 | 8.466 | 8.260 | 8.102 | 7.976 | 7.874 | 7.718 | 7.559 | 7.396 | 7.313 | 7.229 | 7.143 | 7.057 | 6.969 | 6.880 |
| 7 | 12.246 | 9.547 | 8.451 | 7.847 | 7.460 | 7.191 | 6.993 | 6.840 | 6.719 | 6.620 | 6.469 | 6.314 | 6.155 | 6.074 | 5.992 | 5.908 | 5.824 | 5.737 | 5.650 |
零假设前提下,得到如此极短的值得概率非常低,这个12比10%显著性水平的临界F统计量大太多。因此,我们拒绝原假设。
附录如何使用临界 f 值计算器?
首先,这里有一些关于 F 分布概率的临界值 :临界值是特定分布尾部的点,因此这些点到尾部的曲线下面积等于 α 的给定值。因此,对于双尾情况,临界值分别对应左右尾部的两个点,其性质为左尾部曲线下面积(从左临界点算起)与面积之和右尾曲线下等于给定的显着性水平 α。
在左尾情况下,临界值对应于分布左尾的点,其特性是左尾曲线下的面积(从临界点到左边)等于给定的显着性水平 α。
对于右尾情况,临界值对应于分布右尾的点,右尾曲线下的面积(从临界点向右)等于给定的显着性水平 α
我们有一系列临界值计算器,包括 临界 z 值 , 临界的 t值 ,仅举几例。
78相关性和因果性
correlation相关性:A和B有可能被同时观测到或者说B发生时A有可能同时发生
causality因果性:A导致B
79演绎推理deductive reasoning 1
演绎推理:寻找规律或趋势,然后推广。
三段式演绎推理
比如预测小镇人数。
演绎推理(Deductive Reasoning)
演绎推理来自于逻辑学,它是通过一般的原理或规则来推导出特定的结论。如果前提是真的,那么演绎推理的结论就必须是真的。例如,如果所有人都是有死亡的(前提),那么我也会死亡(结论)。这就是一个演绎推理的例子。在演绎推理中,前提的真实性决定了结论的真实性。
归纳推理(Inductive Reasoning)
归纳推理是从特定的实例或例子中发现一般性的规律或原理。归纳推理的结果往往是可能性的,而不是必然性的。例如,如果我看到太阳每天都从东边升起(观察的实例),我可能会推理出太阳每天都会从东边升起(一般规律)。但是,这个结论并不是必然正确的,因为这只是基于我有限的观察得出的。
演绎推理与归纳推理的异同
相同点:两者都是推理的方式,都是通过某种思考过程从一种信息(前提或观察)得出结论。
不同点:演绎推理从一般到特殊,若前提真实,那么结论必然真实;归纳推理从特殊到一般,结论只是可能真实,并非必然真实。另外,演绎推理通常用在数学或逻辑学中,而归纳推理则更常用在科学研究中。
80演绎推理2
解方程,从事实出发,使用逻辑步骤运算或推理,得到其它事实,这里没有推广
81演绎推理3
推导$(x+y)^=x^2+2xy+y^2$
从一个式子出发,使用逻辑步骤运算或推理,得到其它事实
演绎推理是从前提中推导出结论的推理方法。以下是一些演绎推理的例子:
如果所有的狗都会叫,而且这只动物是一只狗,那么它一定会叫。
如果所有的人类都需要呼吸氧气,而且这个人是一个人类,那么他一定需要呼吸氧气。
如果所有蒸汽都会形成云,而且这些白色的云是蒸汽形成的,那么它们一定是蒸汽。
如果所有的矿泉水都含有矿物质,而且这瓶水是矿泉水,那么它一定含有矿物质。
如果所有的植物都需要阳光和水才能生长,而且这颗植物缺乏阳光,那么它无法正常生长。
这些例子展示了演绎推理方法的应用,即从已知的前提中推导出结论。演绎推理可以保证结论的准确性,只要前提是真实的,结论就是正确的。在科学、数学、逻辑等领域中,演绎推理是非常重要的,因为它可以帮助我们得出精确的结论和定理。
82归纳推理inductive reasoning1
找共性
如6, 9, 12, 15……
83归纳推理2
如0, 3, 8, 15, 24,……
找规律推测第n个数是$n^2-1$
首先根据已知数据了解规律,然后推广规律,但这结果不一定正确
84归纳推理3
归纳推理是通过具体的实例来推断出一般规律或结论的推理方法。以下是一些归纳推理的例子:
假设你已经观察到很多鸟都有羽毛,并且你还没有遇到过没有羽毛的鸟,因此你可以归纳出“所有鸟都有羽毛”这一结论。
假设你已经试着用不同的铅笔在不同的纸上写字,你发现所有的铅笔都可以写字,因此你可以归纳出“所有铅笔都可以写字”这一结论。
假设你已经观察到很多人都穿着厚外套在寒冷的天气中行走,并且你还没有遇到过不穿外套的人,因此你可以归纳出“在寒冷的天气中,人们通常穿着厚外套”这一结论。
假设你已经试着用不同的电子设备播放音乐,你发现所有的设备都可以播放音乐,因此你可以归纳出“所有电子设备都可以播放音乐”这一结论。
这些例子说明了归纳推理方法的应用,即通过观察和实验来推断出一般规律或结论。虽然归纳推理不能保证结论的绝对准确性,但在日常生活中,它可以为我们提供很多有用的信息和指导。

