概论

前言

严格来说，我没有读懂这本书，因为我只懂得量子计算的皮毛。

书籍简介

作　者：马鸿洋邱田会王淑梅田艳兵史鹏

出版社：人民邮电出版社

ISBN： 9787115633941

出版时间： 2024-08-01

内容简介

本书系统阐述了量子图像处理及其关键技术。本书内容共分9章，分别介绍了量子图像处理的研究意义和背景与现状、量子图像表示模型、量子图像处理算法、量子图像恢复、量子图像加密、量子水印、量子图像边缘检测、量子图像的分类识别、量子图像仿真实现。本书旨在为量子图像处理领域的科研人员提供具有较强实用性的参考，可作为物理和计算机专业开设量子计算相关课程的教学参考书，也可作为量子计算与量子图像处理的短期专题讲座培训用书。本书结构清晰、内容翔实，对初次接触量子图像处理领域的研究人员，特别是非物理专业的科研技术人员具有一定的参考价值。

作者简介

马鸿洋，2019—2022年山东省物理学类专业及大学物理课程教学指导委员会委员；2018至今教育部高等学校物理学类专业教学指导委员会华东地区工作委员会委员、量子密码委员会委员、中国电子学信息论分委会委员、大数据与智能信息处理技术委员会委员、山东省物理学会理事会理事、山东省光学工程学会理事、青岛市物理学会理事会理事。主要研究方向为网络空间安全、量子保密通信、量子计算、机器学习和深度学习。完成教学科研课题一项，获青岛理工大学优秀科研成果三等奖一项。

邱田会，青岛理工大学副教授。主要研究方向为量子光学和量子信息。主持国家自然科学基金青年基金和理论物理专款各一项，主持山东省自然科学基金培养基金项目一项，作为项目组主要成员参与国家和省部级项目6项。在光的可逆存储、原子相干调控、电磁诱导周期介质性质和应用等方面发表SCI论文20余篇。

正文摘录

第1章绪论

1.1 量子图像处理的研究意义

1.2 量子图像处理的背景与现状

参考文献

第2章量子图像表示模型

2.1 量子图像表示模型及其特点

2.1.1 Qubit Lattice模型

2.1.2 Real Ket模型

2.1.3 Entangled Image模型

2.1.4 FRQI模型

2.1.5 NEQR模型

2.1.6 GQIR模型

2.1.7 NAQSS模型

2.1.8 QRCI模型

2.1.9 QIRHSI模型

2.2 量子图像表示模型分类

2.2.1 量子图像颜色模型

按照颜色信息不同可分为以下几种：

基于二进制的量子图像表示模型
基于灰度
基于RGB
基于红外图像

2.2.2 量子图像坐标模型

利用不同的坐标系捕捉图像信息：

基于笛卡尔坐标系的量子图像表示模型
基于对数极坐标系
基于多维表示

2.3 本章小结

参考文献

第3章量子图像处理算法

3.1 几何变换

本节介绍了基于n个量子比特的标准任意叠加态（NASS）实现图像几何变换。

3.1.1 两点交换

3.1.2 对称翻转

3.1.3 局部翻转

3.1.4 正交旋转

3.2 色彩处理

3.2.1 量子图像的颜色运算

NEQR模型可以方便地处理图像的颜色信息。

3.2.2 伪彩色处理

3.2.3 量子色图

3.2.4 量子伪彩色编码实现

3.3 图像分割

3.3.1 基于量子搜索的图像分割

3.3.2 量子图像分割线路

3.3.3 分割后量子图像的显示

3.4 本章小结

参考文献

第4章量子图像恢复

4.1 量子图像去噪算法

4.1.1 基于NEQR模型的去噪算法

本节主要考虑两种常见噪声，即椒盐噪声和高斯噪声。

本节主要介绍三张图像去噪算法：

Q均值滤波算法：采用均值滤波方法处理椒盐噪声
Q高斯滤波算法：主要用于滤除高斯噪声
Q自适应滤波算法：主要用于处理含有未知噪声的图像

4.1.2 基于量子小波变换的图像去噪方法

Daubechies四阶小波核

Cooley-Tukey FFT

4.2 量子图像复原算法

4.2.1 基于R-L算法的量子图像复原算法

4.2.2 基于约束的最小二乘法滤波的量子图像复原算法

4.3 本章小结

参考文献

第5章量子图像加密

5.1 图像置乱算法

5.1.1 量子仿射变换

量子仿射变换中应用较广泛的是阿诺德变换和斐波那契变换。利用阿诺德变换和斐波那契变换能够将一幅图像置乱，从而使一幅有意义的图像变成一幅毫无意义的图像。

5.1.2 量子Hilbert变换

Hilbert曲线是一种连续的参数曲线，类似于Z曲线、格雷码等。

5.1.3 量子随机行走

马尔可夫过程

5.1.4 骑士巡游变换

模拟骑士在棋盘中的巡游

5.2 图像加密算法

5.2.1 离散余弦变换

5.2.2 DNA编码

5.2.3 混沌映射

Rossler混沌模型
Lorenz混沌模型

5.2.4 量子受控翻转

5.3 量子图像加密方案设计

5.3.1 基于交替量子随机行走和离散余弦变换的图像加解密方案

5.3.2 基于DNA编码与交替量子随机行走的图像加密方案

5.3.3 基于量子随机行走和多维混沌映射的图像加密方案

流程包括以下几个步骤：

图像分割（使用高斯金字塔）
概率矩阵的生成和转化
阿诺德变换置乱
利用欧氏距离和汉明距离求序列
密钥生成
盲水印的嵌入和提取

5.3.4 基于量子受控翻转的图像加密方案

NCQI模型是NEQR模型的改进版

5.4 本章小结

参考文献

第6章量子水印

图像信息隐藏的两大手段包括图像加密和数字水印。

可用于传递秘密信息和版权保护等领域。

6.1 量子信息隐藏

6.1.1 量子LSB算法

6.1.2 量子傅里叶变换

6.1.3 量子小波变换

6.2 量子水印算法

6.2.1 基于量子LSB分块的水印算法

6.2.2 基于量子傅里叶变换的量子水印算法

6.2.3 基于量子Haar小波变换的水印算法

6.2.4 基于莫尔条纹的量子信息隐藏

6.3 本章小结

参考文献

第7章量子图像边缘检测

7.1 图像边缘检测技术

7.1.1 Sobel算子图像边缘检测

7.1.2 Prewitt算子图像边缘检测

7.1.3 Kirsch算子图像边缘检测

7.1.4 Canny算子图像边缘检测

7.2 基于Kirsch算子的量子图像边缘检测算法

7.2.1 算法流程

7.2.2 算法复杂度和仿真结果分析

7.3 基于改进Sobel算子的量子图像边缘检测算法

7.3.1 量子线路设计

7.3.2 算法流程

7.3.3 算法实现

7.3.4 仿真结果与分析

7.4 本章小结

参考文献

第8章量子图像的分类识别

8.1 量子神经网络

8.2 量子卷积神经网络

8.3 基于量子卷积神经网络的手写数字识别

8.3.1 混合量子经典卷积神经网络模型

8.3.2 量子卷积神经网络模型

8.4 本章小结

参考文献

第9章量子图像仿真实现

根据不同的后端处理系统，量子软件开发工具分为两大类：一类是可以访问量子处理器的SDK，另一类是基于量子计算模拟器的SDK。

由于量子图像多来自经典世界，需要将经典图像编码为量子信息后再进行处理，而目前尚无可有效完成此项工作的量子计算机，因此量子图像需要通过基于量子计算模拟器的SDK来进行仿真实现。

9.1 主流量子仿真SDK介绍

Qiskit
QPanda
Azure Quantum（Q#）

9.2 FRQI和NEQR量子图像的仿真

9.2.1 制备FRQI图像量子态

9.2.2 四像素灰度FRQI图像仿真实现

9.2.3 制备NEQR量子态

9.2.4 四像素灰度NEQR图像仿真实现

9.3 小图像和大图像的量子边缘检测QHED算法

9.3.1 量子概率图像编码

9.3.2 量子Hadamard边缘检测

9.4 本章小结

参考文献

附录量子计算编程入门内容总结-Qiskit

1. 基础知识与前言

除了理论内容之外，在量子SDK (Quantum Software Development Kit) 上对于程序和算法的实现同样重要，本文将以之前文章的内容为基础探索Qiskit的使用方法：

Mercury：量子计算入门内容总结501 赞同 · 14 评论文章

同样，在开始正式学习Qiskit之前，我们需要一些基本的计算机知识，熟悉的同学可以直接跳过这个章节，这里我们主要是基于Python来编程。

1.1. 在官网上下载Python和Qiskit开发工具包

笔者主要使用的是Anaconda Python，可以在官网上直接下载；之后在terminal中输入 (笔者使用的是macOS系统) 来下载Qiskit开发工具包：

1
pip install qiskit

之后我们可以在terminal中通过输入如下的代码跳转到Jupyter Notebook的页面，Jupyter Notebook可能是结合编程、文本和图像的最佳方式：

1
jupyter notebook

在Jupyter Notebook创建一个新文件之后输入如下的代码我们便可以检验是否下载好并且是否下载了最新的版本：

1
2
import qiskit
qiskit.__qiskit_version__

这里我的输出结果为如下所示，说明我的版本为0.45.0，在Qiskit官网上可以发现是截止这篇文章发布前的最新版。

1
{'qiskit': '0.45.0', 'qiskit-aer': '0.13.0', 'qiskit-ignis': None, 'qiskit-ibmq-provider': '0.20.2', 'qiskit-nature': None, 'qiskit-finance': None, 'qiskit-optimization': None, 'qiskit-machine-learning': None}

之后我们需要在IBM的官网上注册账号来获取API代码，这是我们和IBM的量子计算机链接的途径，在个人主页中找到后复制到如下的代码中，我们就可以把我们在自己电脑上创建的量子电路传输给IBM的量子计算机并得到结果。

1
2
3
from qiskit import IBMQ
IBMQ.save_account('在这里输入你的API代码')
IBMQ.load_account()

1.2. Python基础知识

这里的内容不是本文的重点，以下的内容默认读者对Python中的基础语法有所掌握。

1.3. 量子计算基础知识

在之前的内容中，我们学习了使用态叠加原理来表示一个量子比特的状态，即用以和为基向量的线性组合来表示，那么我们如何在Qiskit开发工具包中表示这个状态呢？首先我们引入我们需要使用的工具：

1
2
3
from qiskit import QuantumCircuit, assemble, Aer
from qiskit.visualization import plot_histogram, plot_bloch_vector
from math import sqrt, pi

其次我们建立一个单量子比特的电路，通过之前的学习我们知道一个量子比特总是以开始的，在Qiskit中我们可以使用initialize()将它转化成任何状态。比如在这里我们将输入进去，并告诉它哪一个量子比特是我们想初始化的：

1
2
3
4
qc = QuantumCircuit(1)  # 建立一个单量子比特电路
initial_state = [0,1]   # 定义初始状态 |1>
qc.initialize(initial_state, 0) # 对第0个量子比特应用初始化的操作
qc.draw()  # 通过这条指令可以展示我们设置的量子电路

之后我们可以使用Qiskit的模拟器来查看量子比特的最终状态，为了从电路中获得结果，我们使用run来执行电路，最后我们可以通过.result()来获得结果。

1
2
3
4
5
6
sim = Aer.get_backend('aer_simulator')  # 告诉Qiskit如何模拟我们的电路
qc.save_statevector()   # 告诉模拟器保存statevector
qobj = assemble(qc)     # 从电路中创建一个Qobj来给模拟器进行模拟
result = sim.run(qobj).result() # 进行模拟并显示结果
out_state = result.get_statevector()
print(out_state) # 用statevector的形式展示最后的结果

我最后得到如下的结果：Python通常通过来表示复数里的，因此我这里得到的。

1
2
Statevector([0.+0.j, 1.+0.j],
            dims=(2,))

现在让我们像真正的量子计算机那样测量我们的量子比特并观察我们可以得到的结果：

1
2
qc.measure_all()
qc.draw()

我们可以得到这样的图像：

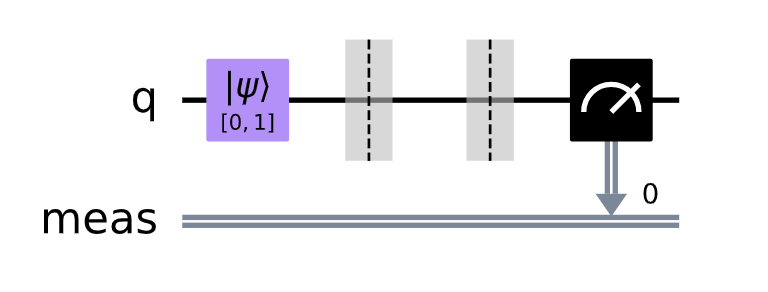
我们得到的量子电路

为了和之前得到的statevector结果不一样，我们可以使用.get_counts()来获得测量出0和1的数量：

1
2
3
4
qobj = assemble(qc)
result = sim.run(qobj).result()
counts = result.get_counts()
plot_histogram(counts)

从得到的结果中我们看出，我们100%会测量出。

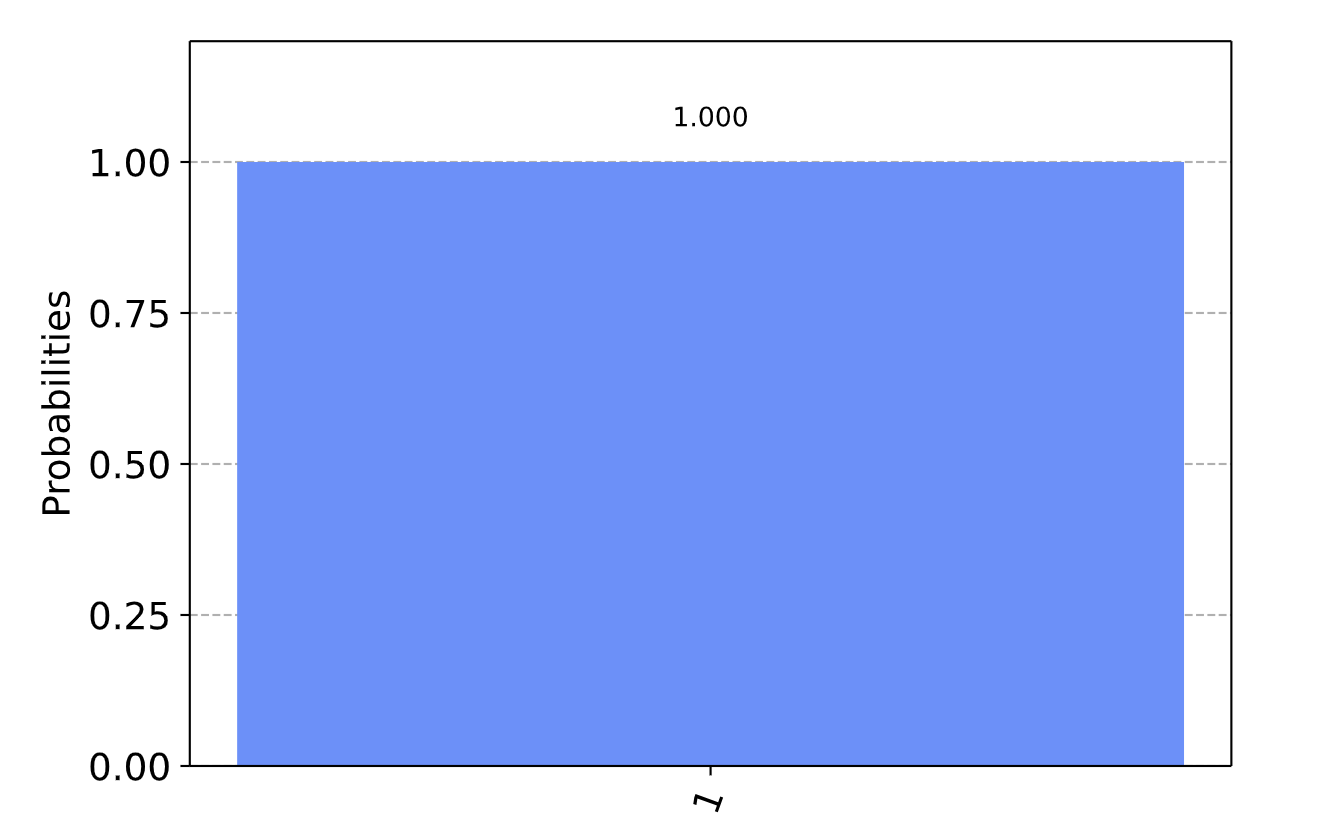
我们得到的测量结果

接下来如果我们将输入的状态换成叠加态，看看会发生什么？

1
2
3
4
5
6
7
initial_state = [1/sqrt(2), 1j/sqrt(2)]  # 定义状态 |q_0>
qc = QuantumCircuit(1) # 我们必须重新定义qc
qc.initialize(initial_state, 0) # 对第0个量子比特应用初始化的操作
qc.save_statevector() # 保存statevector
qobj = assemble(qc)
state = sim.run(qobj).result().get_statevector() # 执行电路
print(state)           # 输出结果

之后我们可以得到如下的结果，并重复以上的操作，我们可以得到测量的结果，即我们有50%的几率测量出，也有50%的几率测量出。

1
2
3
qobj = assemble(qc)
results = sim.run(qobj).result().get_counts()
plot_histogram(results)

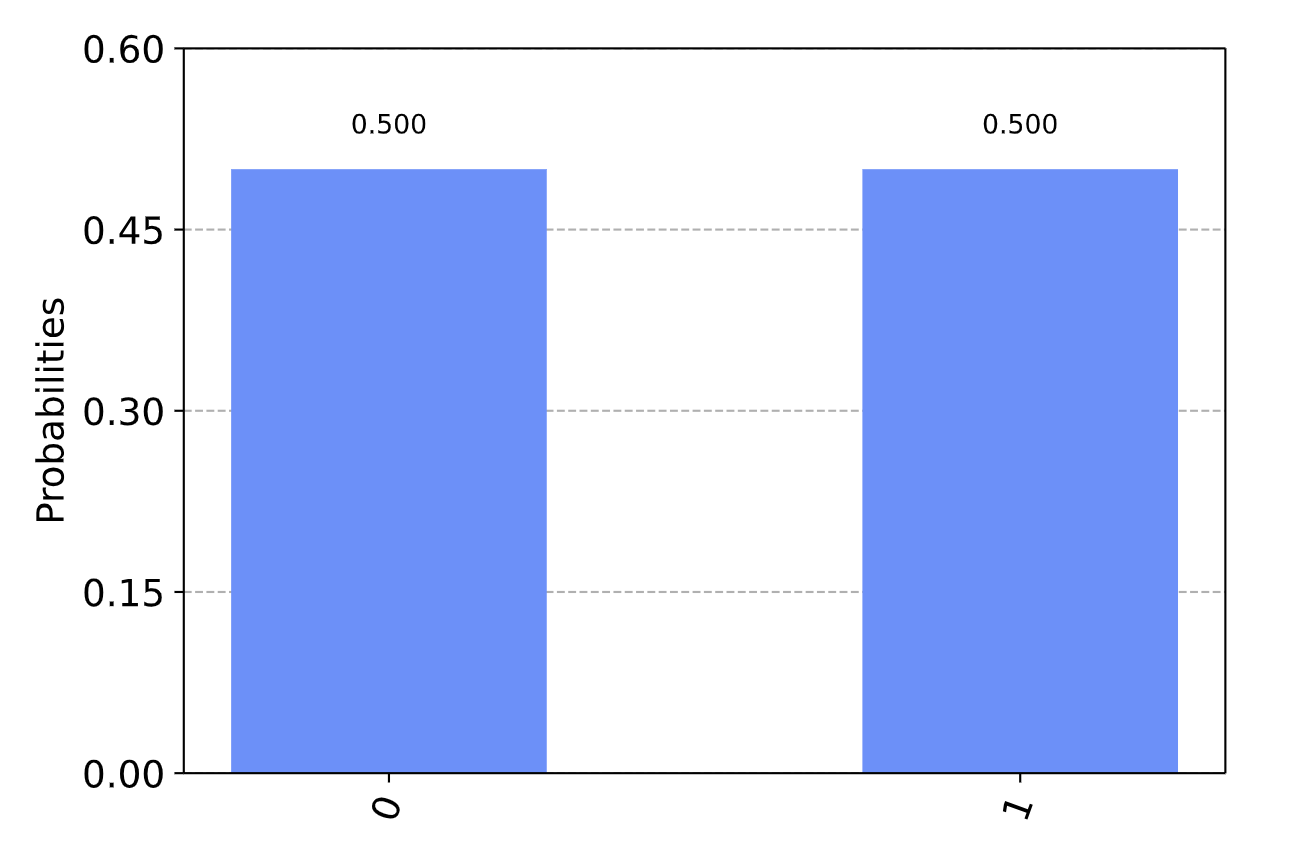
我们得到的测量结果

在之前我们同样也学习了布洛赫球(Bloch sphere) 的表达形式，那么我们怎么使用Qiskit来形象的表示布洛赫球呢？首先我们需要通过如下的代码安装’qiskit_textbook’模块：

1
pip install git+https://github.com/qiskit-community/qiskit-textbook.git#subdirectory=qiskit-textbook-src

之后我们再使用如下的代码就可以表示布洛赫球了，这里我们定义 (注意这里可能需要根据情况从math中引入pi或者从numpy库中导入)：

1
2
3
from qiskit_textbook.widgets import plot_bloch_vector_spherical
coords = [pi/2,0,1] # 输入[Theta, Phi, Radius]
plot_bloch_vector_spherical(coords) # 布洛赫向量

我们可以得到如下的结果：

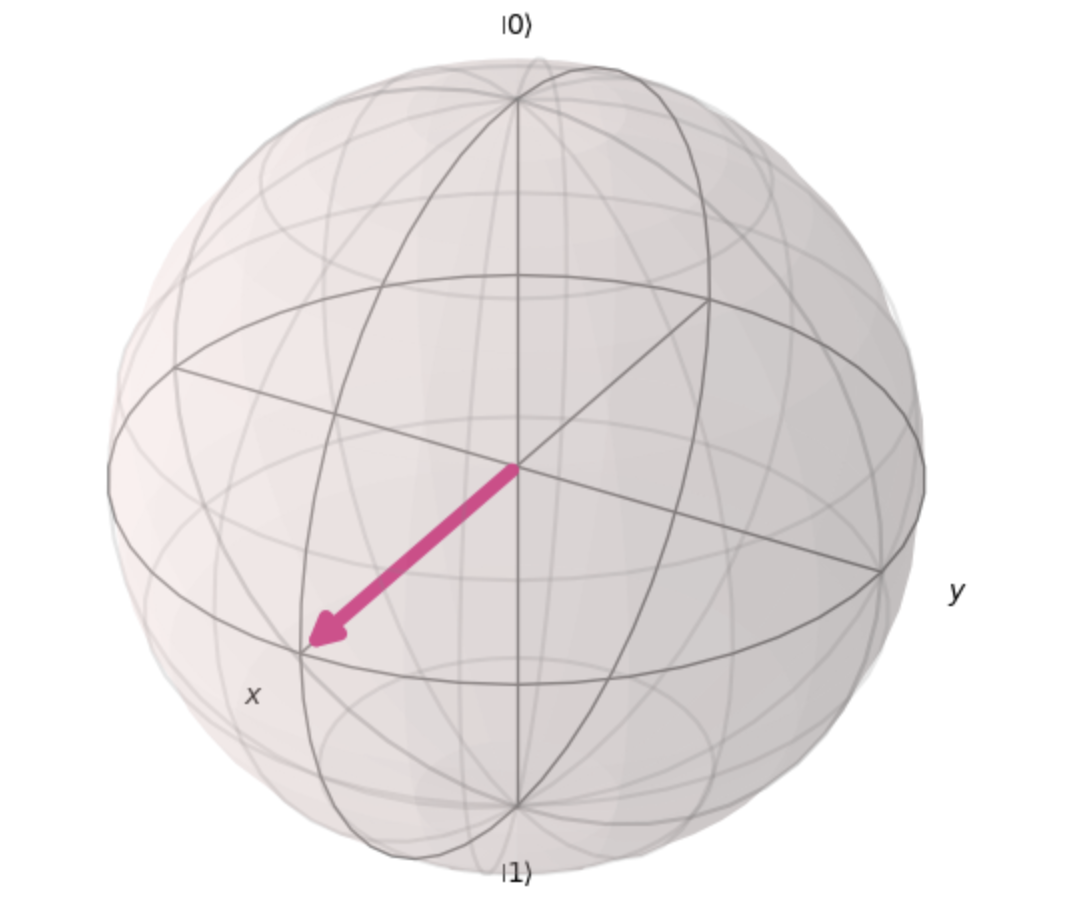
我们得到的结果

除了对量子比特的描述之外，我们在之前的内容里也了解了很多有关单比特量子门的内容，我们下面就具体看一下如何在Qiskit中表示量子门，首先是最常见的门，门和门，我们可以用如下的形式来表示：

1
2
3
qc = QuantumCircuit(1) # 首先我们先创建一个单量子比特电路
qc.x(0) # 在第0个量子比特上放上X门
qc.draw() # 画出我们设计的电路

我们可以得到：

我们得到的结果

类似的，我们可以在同样的一条电路上放上门和门：

1
2
3
4
5
from qiskit_textbook.widgets import gate_demo
gate_demo(gates='pauli')
qc.y(0) # 在第0个量子比特上放上Y门
qc.z(0) # 在第0个量子比特上放上Z门
qc.draw()

我们可以得到：

我们得到的结果

类似的，我们接着引入门和门：

1
2
from qiskit_textbook.widgets import gate_demo
gate_demo(gates='pauli+h+p')

在Qiskit中，我们通常通过两个变量来描述门：

1
2
3
qc = QuantumCircuit(1)
qc.p(pi/4, 0) # 前面一个数字用来表示phi，后面一个数字来表示需要操作的量子比特
qc.draw()

我们可以得到：

我们得到的结果

以上就是一些常用的量子系统的状态和量子门的表达方式，这里的内容肯定不是足够详尽的，如果在实际使用中遇到了不常见的情况，我们可以通过登陆Qiskit或者IBM的官网进行查询。

2. 从传统算法到量子算法

2.1. Deutsch-Jozsa算法

在之前的内容中，我们介绍了D-J算法的使用场景和主要结构，D-J算法为了解决判断输入的函数为常函数还是平衡函数而诞生。那么如果我们想要在Qiskit中运行，我们应该怎么做呢？在本文的例子中，我们针对以下函数进行算法的撰写，具体算法是怎么写出来的，不是本文的重点内容，这里我们重点关注如何在Qiskit中实现：

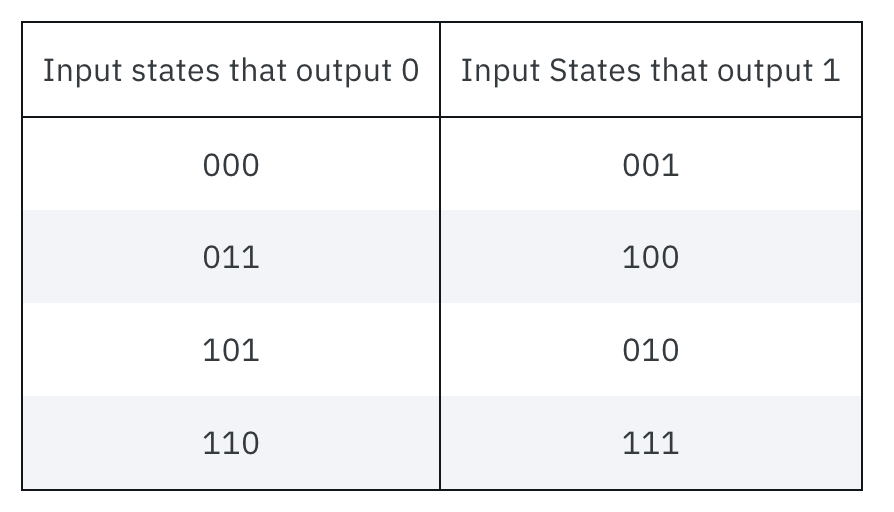
第一步我们要初始化所有的量子比特以满足D-J算法的需求：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
dj_circuit = QuantumCircuit(n+1, n)

# 应用H门
for qubit in range(n):
    dj_circuit.h(qubit)

# 将最底部的量子比特转化成 |->
dj_circuit.x(n)
dj_circuit.h(n)
dj_circuit.draw()

第二步我们要加上预言机里的量子门：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
dj_circuit = QuantumCircuit(n+1, n)

# 应用H门
for qubit in range(n):
    dj_circuit.h(qubit)

# 将最底部的量子比特转化成 |->
dj_circuit.x(n)
dj_circuit.h(n)

# 增加预言机里的量子门
dj_circuit = dj_circuit.compose(balanced_oracle)
dj_circuit.draw()

最后我们要根据算法的结构在n个量子比特上加入门，并测量所有输入的量子寄存器：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
dj_circuit = QuantumCircuit(n+1, n)

# 应用H门
for qubit in range(n):
    dj_circuit.h(qubit)

# 将最底部的量子比特转化成 |->
dj_circuit.x(n)
dj_circuit.h(n)

# 增加预言机里的量子门
dj_circuit = dj_circuit.compose(balanced_oracle)

# 重复H门
for qubit in range(n):
    dj_circuit.h(qubit)
dj_circuit.barrier()

# 测量
for i in range(n):
    dj_circuit.measure(i, i)

# 表示电路
dj_circuit.draw()

于是我们可以得到：

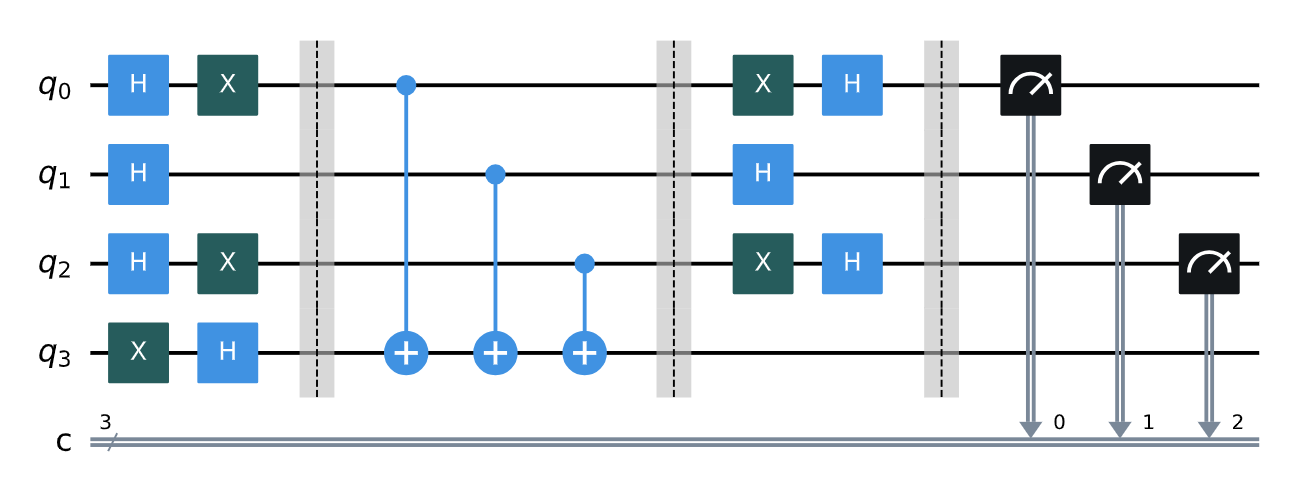
D-J算法

如果我们想得到测量的结果，我们可以重复上面学习过的使用量子模拟器的方法：

1
2
3
4
5
aer_sim = Aer.get_backend('aer_simulator')
results = aer_sim.run(dj_circuit).result()
answer = results.get_counts()

plot_histogram(answer)

我们可以得到结果：

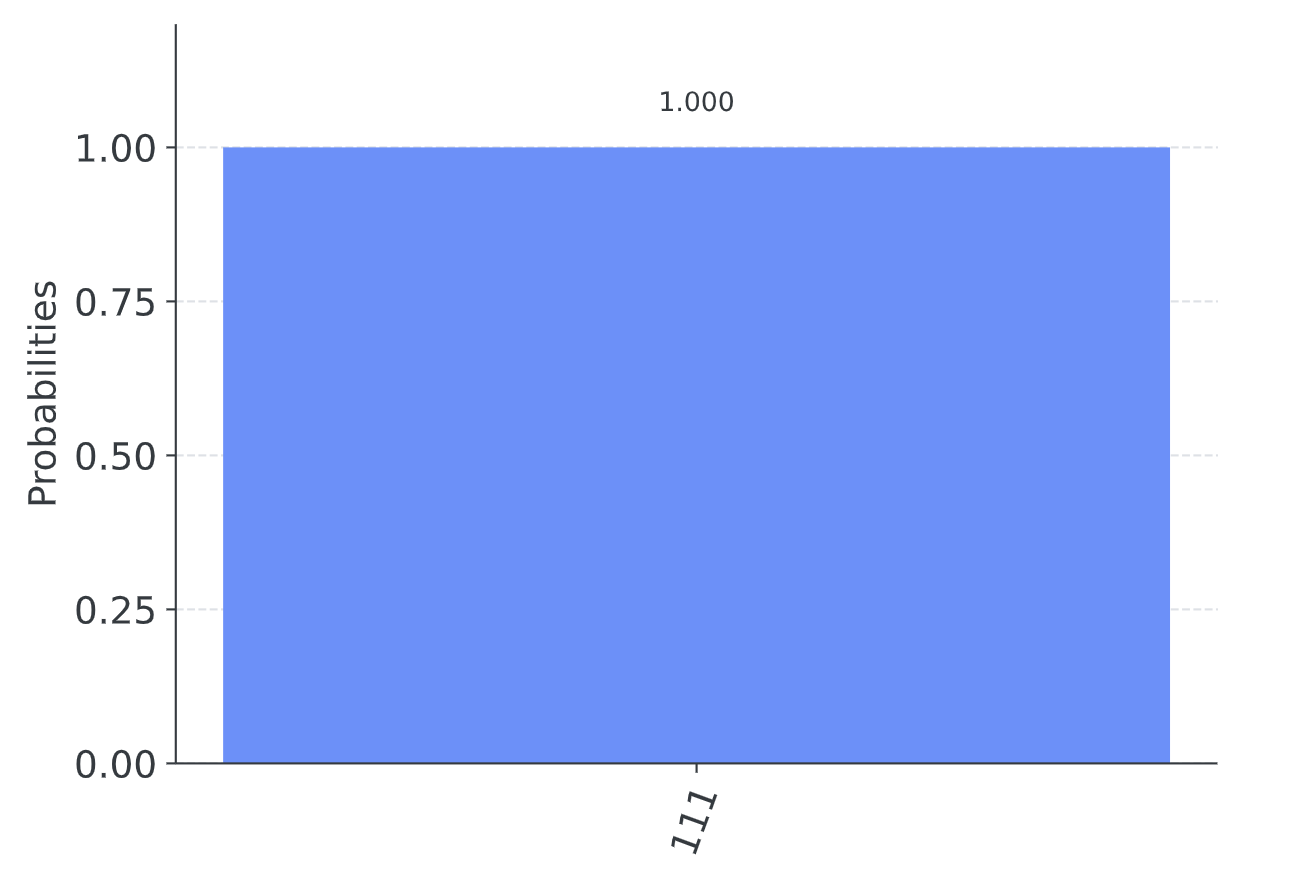
我们得到的结果

根据我们之前学习的内容，如果所有量子比特的测量结果都为0，那么这个函数就可以判断为常函数；如果我们得到任何0之外的结果，那么这个函数就可以判断为平衡函数。从我们得到的结果我们可以很明显看出这个函数为平衡函数。

2.2. Simon算法

在之前的学习中我们了解了Simon算法的使用场景和基本结构，那么我们怎么在Qiskit中实现Simon算法呢？我们这里可以直接通过simon_oracle创造一个Simon算法的预言机，在这里的例子里，我们假设。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
# 引入Qiskit的各类工具
from qiskit import IBMQ, Aer
from qiskit.providers.ibmq import least_busy
from qiskit import QuantumCircuit, transpile

from qiskit.visualization import plot_histogram
from qiskit_textbook.tools import simon_oracle

b = '110'

n = len(b)
simon_circuit = QuantumCircuit(n*2, n)

# 根据Simon算法的结构应用H门
simon_circuit.h(range(n))    
    
# 在这里增加barrier以区分不同区域
simon_circuit.barrier()

# 这里我们直接通过simon_oracle创造一个simon算法的预言机
simon_circuit = simon_circuit.compose(simon_oracle(b))

# 在这里增加barrier以区分不同的区域
simon_circuit.barrier()

# 根据Simon算法的结构应用H门
simon_circuit.h(range(n))

# 测量量子比特
simon_circuit.measure(range(n), range(n))
simon_circuit.draw()

我们在这里得到的结果为：

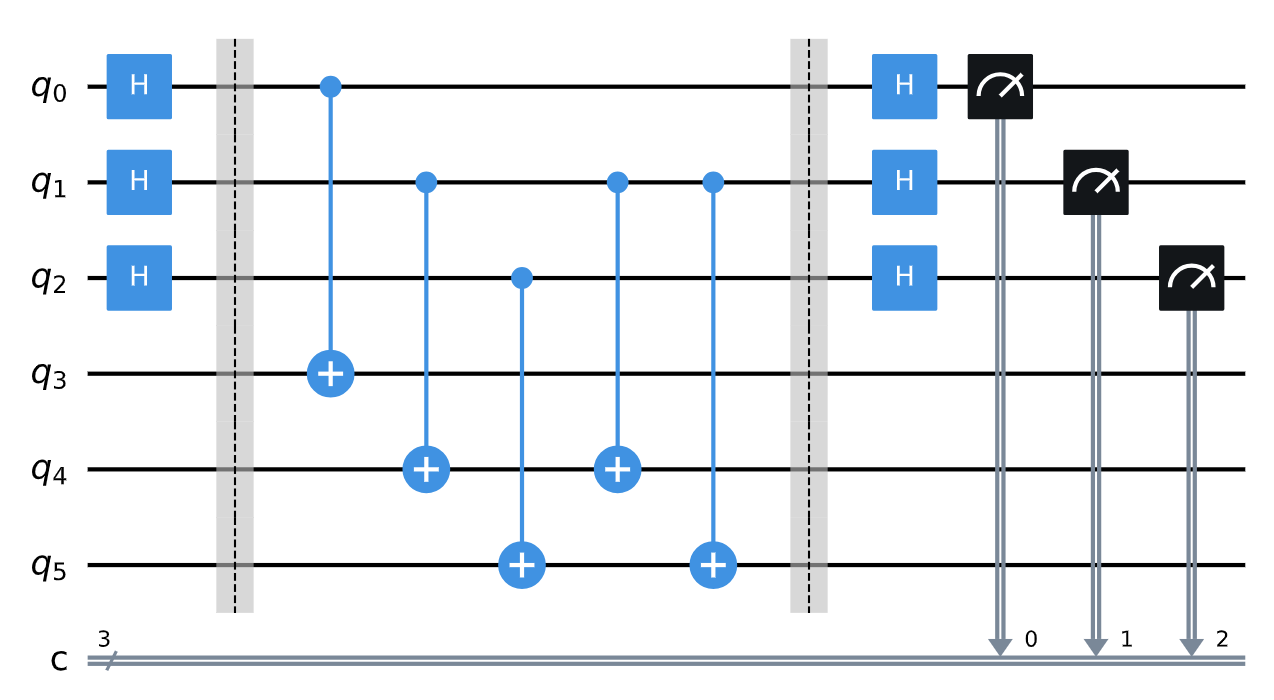
我们在这里得到的结果

类似的，我们可以通过使用量子模拟器来得到测量的结果：

1
2
3
4
aer_sim = Aer.get_backend('aer_simulator')
results = aer_sim.run(simon_circuit).result()
counts = results.get_counts()
plot_histogram(counts)

于是我们可以得到如下的结果，之后我们再应用传统算法就可以得到最后的结果：

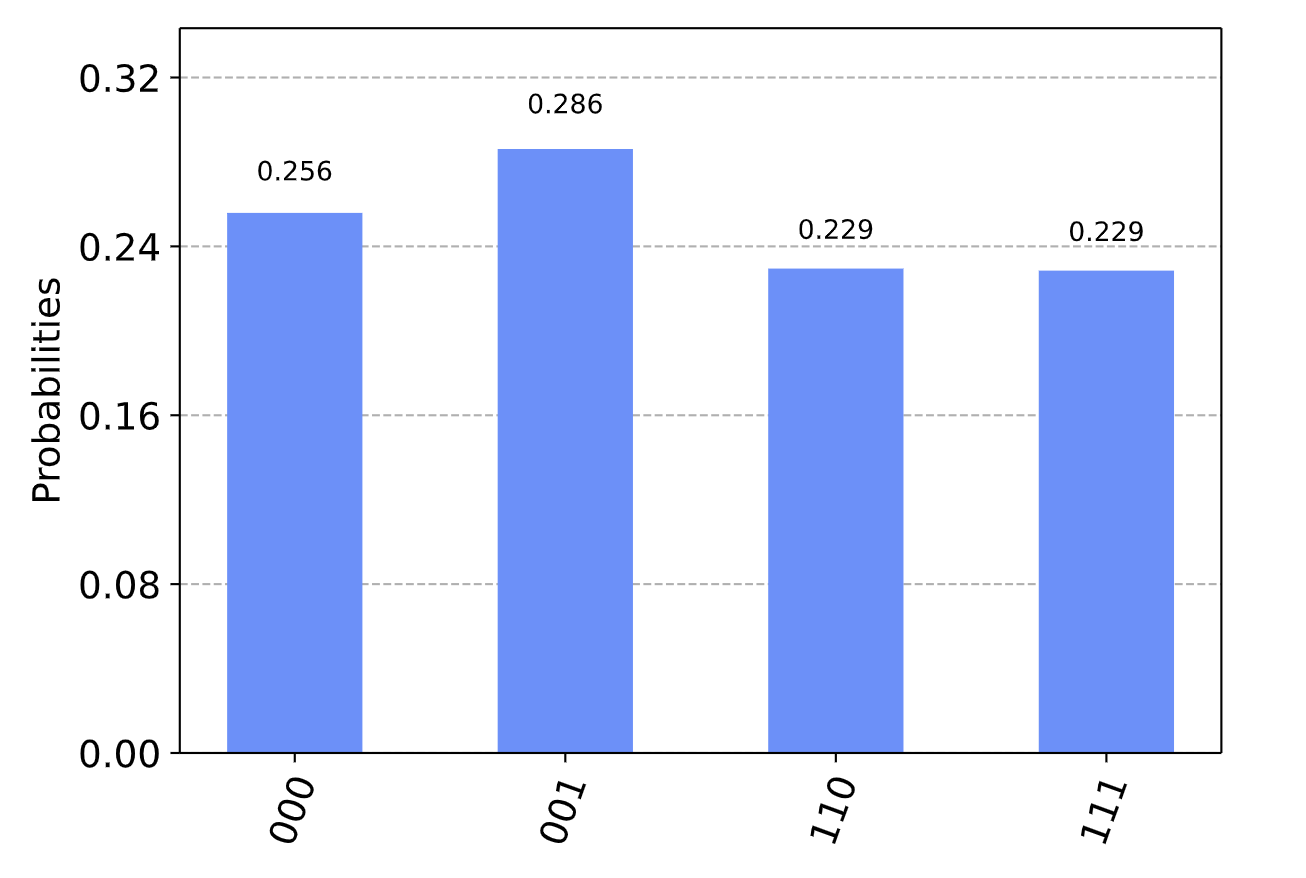
在之前的内容中，我们同样引入了Shor算法、Grover算法和QAOA算法，由于这几个算法涉及量子傅里叶变换 (Quantum Fourier Transform)和QPE算法 (Quantum Phase Estimation)，我之后会针对这个内容做一个专题进行解释和总结。

3. 量子计算在密码学中的应用

3.1. 量子密钥分发 (QKD)

我们在之前的内容中介绍了量子密钥分发的原理，即如果Alice希望发送给Bob一个量子比特，但窃听者试图在Bob之前测量这个量子比特，那么窃听者的测量有可能改变量子比特的状态，而Bob将接收不到Alice发送的量子比特的状态。假设Alice希望用x基来表示，并将其发给Bob，如果Bob同样用x基来进行解密，那么他一定会得到，在Qiskit我们这样表示：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
from qiskit import QuantumCircuit, Aer, transpile
from qiskit.visualization import plot_histogram, plot_bloch_multivector
from numpy.random import randint
import numpy as np

qc = QuantumCircuit(1,1)
# Alice 将量子比特转换成|+>来发送
qc.h(0)
qc.barrier()
# Alice 现在把这个量子比特发送给Bob
# Bob 使用相同的基来进行测量
qc.h(0)
qc.measure(0,0)

# 画出并模拟电路
display(qc.draw())
aer_sim = Aer.get_backend('aer_simulator')
job = aer_sim.run(qc)
plot_histogram(job.result().get_counts())

我们可以得到：

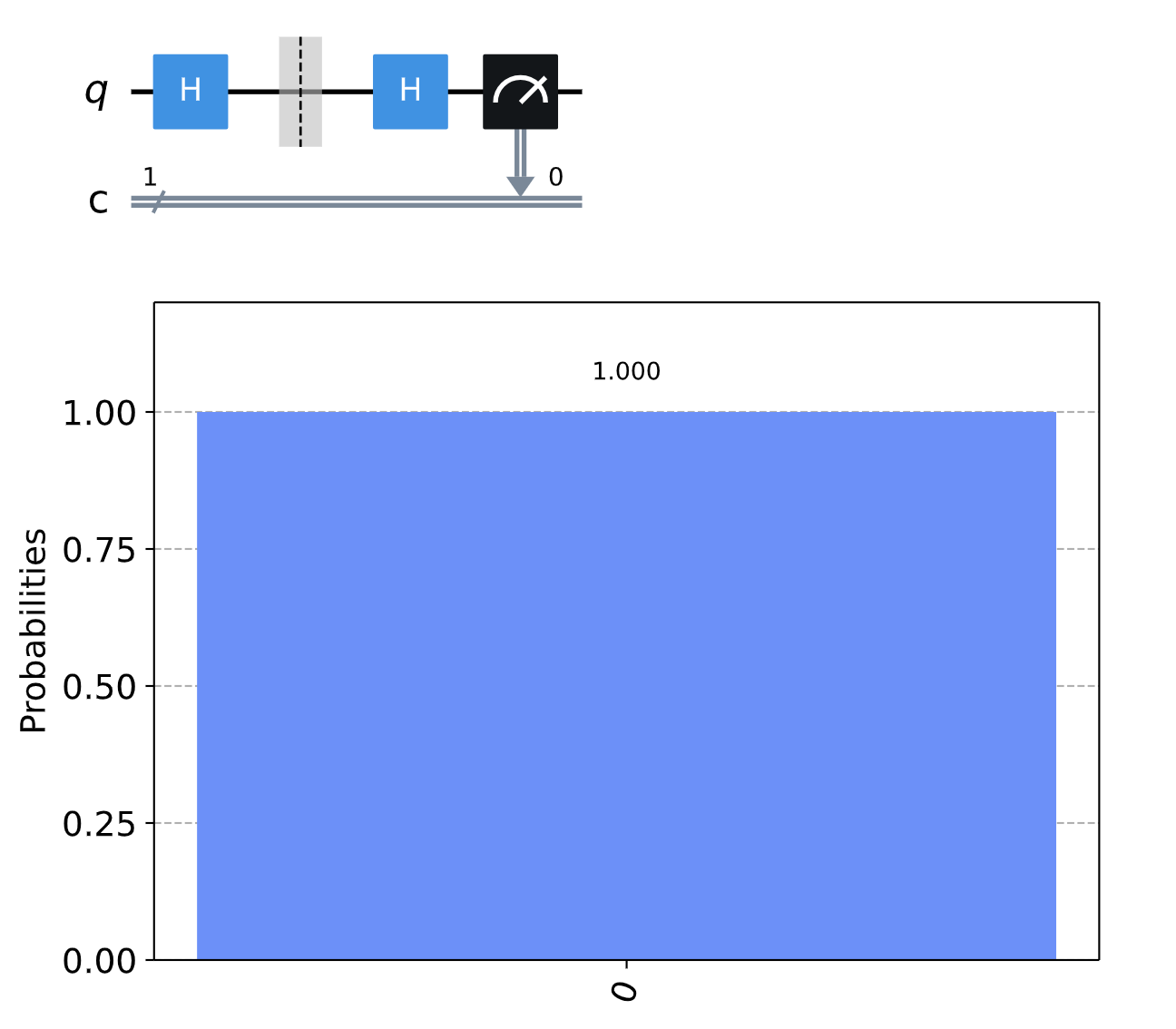
我们得到的结果

通过之前的学习我们知道，如果窃听者在Bob之前尝试通过z基测量，那么Bob就不会一定得到。在Qiskit中我们这样表示：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
qc = QuantumCircuit(1,1)
# Alice 将量子比特转换成|+>来发送
qc.h(0)
# Alice 现在把这个量子比特发送给Bob
# 但是窃听者尝试阅读这个消息
qc.measure(0, 0)
qc.barrier()
# 窃听者在解密后将结果传达给Bob
# Bob用x基来进行解密
qc.h(0)
qc.measure(0,0)

# 画出并模拟电路
display(qc.draw())
aer_sim = Aer.get_backend('aer_simulator')
job = aer_sim.run(qc)
plot_histogram(job.result().get_counts())

我们可以得到如下的结果：

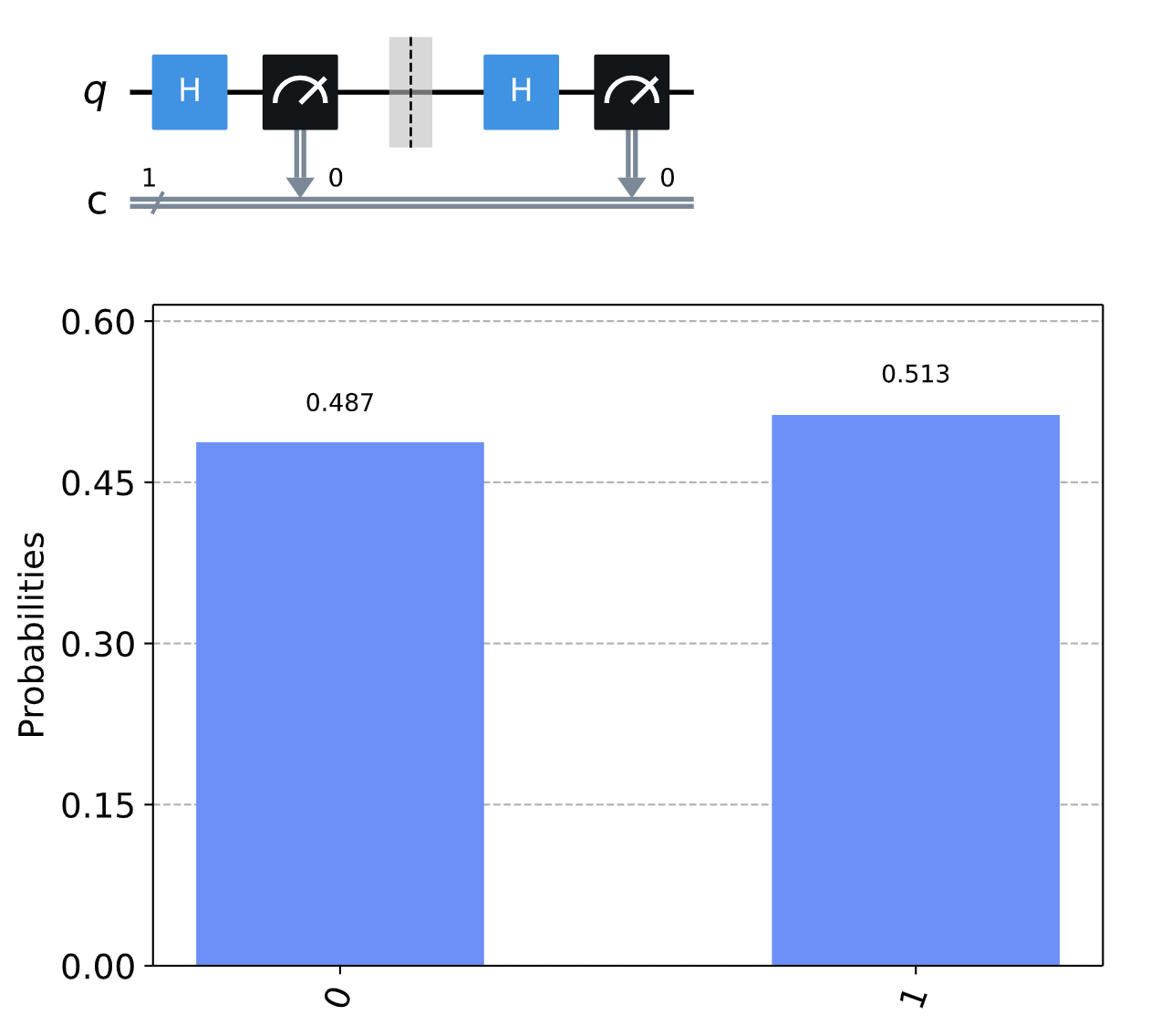
我们得到的结果

从结果中我们可以观察到，Bob测量出的概率仅剩50%左右。

4. 量子机器学习

由于篇幅限制，之后我会针对量子机器学习的内容做一个专题进行解释和总结。

声明：本文的主要内容为针对Qiskit中提供的教程进行的总结

概论#

前言#

书籍简介#

内容简介#

作者简介#

正文摘录#

第1章 绪论#

1.1 量子图像处理的研究意义#

1.2 量子图像处理的背景与现状#

参考文献#

第2章 量子图像表示模型#

2.1 量子图像表示模型及其特点#

2.1.1 Qubit Lattice模型#

2.1.2 Real Ket模型#

2.1.3 Entangled Image模型#

2.1.4 FRQI模型#

2.1.5 NEQR模型#

2.1.6 GQIR模型#

2.1.7 NAQSS模型#

2.1.8 QRCI模型#

2.1.9 QIRHSI模型#

2.2 量子图像表示模型分类#

2.2.1 量子图像颜色模型#

2.2.2 量子图像坐标模型#

2.3 本章小结#

参考文献#

第3章 量子图像处理算法#

3.1 几何变换#

3.1.1 两点交换#

3.1.2 对称翻转#

3.1.3 局部翻转#

3.1.4 正交旋转#

3.2 色彩处理#

3.2.1 量子图像的颜色运算#

3.2.2 伪彩色处理#

3.2.3 量子色图#

3.2.4 量子伪彩色编码实现#

3.3 图像分割#

3.3.1 基于量子搜索的图像分割#

3.3.2 量子图像分割线路#

3.3.3 分割后量子图像的显示#

3.4 本章小结#

参考文献#

第4章 量子图像恢复#

4.1 量子图像去噪算法#

4.1.1 基于NEQR模型的去噪算法#

4.1.2 基于量子小波变换的图像去噪方法#

4.2 量子图像复原算法#

4.2.1 基于R-L算法的量子图像复原算法#

4.2.2 基于约束的最小二乘法滤波的量子图像复原算法#

4.3 本章小结#

参考文献#

第5章 量子图像加密#

5.1 图像置乱算法#

5.1.1 量子仿射变换#

5.1.2 量子Hilbert变换#

5.1.3 量子随机行走#

5.1.4 骑士巡游变换#

5.2 图像加密算法#

5.2.1 离散余弦变换#

5.2.2 DNA编码#

5.2.3 混沌映射#

5.2.4 量子受控翻转#

5.3 量子图像加密方案设计#

5.3.1 基于交替量子随机行走和离散余弦变换的图像加解密方案#

5.3.2 基于DNA编码与交替量子随机行走的图像加密方案#

5.3.3 基于量子随机行走和多维混沌映射的图像加密方案#

5.3.4 基于量子受控翻转的图像加密方案#

5.4 本章小结#

参考文献#

第6章 量子水印#

6.1 量子信息隐藏#

6.1.1 量子LSB算法#

6.1.2 量子傅里叶变换#

6.1.3 量子小波变换#

6.2 量子水印算法#

6.2.1 基于量子LSB分块的水印算法#

6.2.2 基于量子傅里叶变换的量子水印算法#

6.2.3 基于量子Haar小波变换的水印算法#

6.2.4 基于莫尔条纹的量子信息隐藏#

概论

前言

书籍简介

内容简介

作者简介

正文摘录

第1章绪论

1.1 量子图像处理的研究意义

1.2 量子图像处理的背景与现状

参考文献

第2章量子图像表示模型

2.1 量子图像表示模型及其特点

2.1.1 Qubit Lattice模型

2.1.2 Real Ket模型

2.1.3 Entangled Image模型

2.1.4 FRQI模型

2.1.5 NEQR模型

2.1.6 GQIR模型

2.1.7 NAQSS模型

2.1.8 QRCI模型

2.1.9 QIRHSI模型

2.2 量子图像表示模型分类

2.2.1 量子图像颜色模型

2.2.2 量子图像坐标模型

2.3 本章小结

参考文献

第3章量子图像处理算法

3.1 几何变换

3.1.1 两点交换

3.1.2 对称翻转

3.1.3 局部翻转

3.1.4 正交旋转

3.2 色彩处理

3.2.1 量子图像的颜色运算

3.2.2 伪彩色处理

3.2.3 量子色图

3.2.4 量子伪彩色编码实现

3.3 图像分割

3.3.1 基于量子搜索的图像分割

3.3.2 量子图像分割线路

3.3.3 分割后量子图像的显示

3.4 本章小结

参考文献

第4章量子图像恢复

4.1 量子图像去噪算法

4.1.1 基于NEQR模型的去噪算法

4.1.2 基于量子小波变换的图像去噪方法

4.2 量子图像复原算法

4.2.1 基于R-L算法的量子图像复原算法

4.2.2 基于约束的最小二乘法滤波的量子图像复原算法

4.3 本章小结

参考文献

第5章量子图像加密

5.1 图像置乱算法

5.1.1 量子仿射变换

5.1.2 量子Hilbert变换

5.1.3 量子随机行走

5.1.4 骑士巡游变换

5.2 图像加密算法

5.2.1 离散余弦变换

5.2.2 DNA编码

5.2.3 混沌映射

5.2.4 量子受控翻转

5.3 量子图像加密方案设计

5.3.1 基于交替量子随机行走和离散余弦变换的图像加解密方案

5.3.2 基于DNA编码与交替量子随机行走的图像加密方案

5.3.3 基于量子随机行走和多维混沌映射的图像加密方案

5.3.4 基于量子受控翻转的图像加密方案

5.4 本章小结

参考文献

第6章量子水印

6.1 量子信息隐藏

6.1.1 量子LSB算法

6.1.2 量子傅里叶变换

6.1.3 量子小波变换

6.2 量子水印算法

6.2.1 基于量子LSB分块的水印算法

6.2.2 基于量子傅里叶变换的量子水印算法

6.2.3 基于量子Haar小波变换的水印算法

6.2.4 基于莫尔条纹的量子信息隐藏