概论
前言
本书值得做神经计算方向的人阅读。
因为本书内容比较硬核,这里只贴章节小结。
相关代码链接如下所示:
First Training Course on Neural Modeling and Programming (第一届神经计算建模及编程培训班)
书籍简介
作者: 王超名
出版社: 电子工业出版社
出版年: 2023-6
ISBN: 9787121389238
内容简介
计算神经科学作为脑科学与人工智能之间的桥梁,是一门高速发展的新兴交叉学科。本书采用理论与实践结合的方式为读者讲述计算神经科学的基础知识。它从基础的数学和物理原理出发,详细介绍了各类神经元模型、突触模型,以及具有不同结构和功能的网络模型,如兴奋﹣抑制平衡网络、决策网络、连续吸引子网络、库网络等。本书不仅讲解了理论知识,还基于 BrainPy(专门针对计算神经科学设计的编程框架)提供了实践代码,使读者能够动手模拟和分析神经系统的行为和性质。本书既可以作为计算神经科学的教材,也可以作为对该领域感兴趣的读者的参考书。
作者简介
王超名,北京大学心理与认知科学学院博雅博士后。于2018年获得北京交通大学工学学士学位,2023年获得北京大学理学博士学位。研究领域是计算认知神经科学与大规模脑仿真。通用脑动力学编程框架BrainPy的发起人与主理人。
陈啸宇,加拿大多伦多大学生理系博士研究生。于2021年获得清华大学理学学士学位,曾于北京大学神经信息处理实验室担任科研助理。研究领域是神经生物学和计算认知神经科学。
张天秋,北京大学前沿交叉学科研究院博士研究生。于2022年获得北京邮电大学工学学士学位。研究领域是计算认知神经科学与大规模脑仿真。
吴思,北京大学心理与认知科学学院教授,IDG麦戈文脑科学研究所、定量生物学中心、北京大学―清华大学生命科学联合中心研究员,北京智源学者。研究领域是计算认知神经科学和类脑计算。
正文摘录
第 1 篇 基础知识
第 1 章 编程基础知识
1.1 安装教程
1.1.1 Linux 与macOS 系统
1.1.2 Windows 系统
1.1.3 更新版本和环境
1.2 JIT 编译下的编程基础
1.2.1 JIT 编译加速
1.2.2 数据操作
1.2.3 控制流
1.3 动力学模型的编程基础
1.3.1 积分器
1.3.2 更新函数
1.3.3 突触计算
1.3.4 运行器
1.4 查阅文档
1.5 本章小结
本章主要介绍了脑动力学模型通用编程软件BrainPy的安装教程和使用方法。BrainPy通过JIT编译技术大幅提高了模型的运行速度,使得模拟大规模脑动力学模型成为可能。在JIT编译框架下,数据操作和控制流与传统框架不同,BrainPy提供了方便易懂的新接口,可以帮助用户更轻松地编程,填补了 JIT 编译带来的不便。本章还介绍了进行动力学模型编程所需要了解的基本要素,包括积分器、更新函数、突触计算和运行器。这些基本要素将帮助我们搭建和运行各种动力学模型。在后续章节中,我们会对神经元模型、突触及突触可塑性模型、神经网络模型进行介绍。
第 2 篇 神经元模型
第 2 章 神经元的电导模型
2.1 神经元结构
2.2 静息膜电位
2.3 等效电路
2.4 电缆方程
2.4.1 电缆方程的推导
2.4.2 电信号在长直纤维中的被动传播
2.5 动作电位
2.5.1 动作电位的定义
2.5.2 动作电位的产生机制
2.5.3 动作电位的远距离传播
2.6 霍奇金—赫胥黎(HH)模型
2.6.1 离子通道模型
2.6.2 利用电压钳技术测量离子电流
2.6.3 泄漏电流的测量
2.6.4 INa 和IK 的测量
2.6.5 HH 模型的数学表达
2.7 HH 模型的编程实现
2.8 本章小结
本章主要介绍了神经元的电导模型,从生物学角度对神经元进行建模。第一,简单介绍了神经元结构;第二,通过Nernst方程和GHK方程引入了离子通道的平衡电位和细胞膜的静息电位的概念;第三,我们尝试得出神经元的等效电路;第四,根据长直神经纤维的等效电路,推导电缆方程,了解到电信号在神经元中被动传播会快速衰减。为了有效传输电信号,生物系统通过电压门控的离子产生动作电位,并利用郎飞结保证电信号的远距离传播。为了描述动作电位的产生机制,Hodgkin和Huxley提出了HH模型。他们对神经元细胞膜上的钠离子通道、钾离子通道和泄露通道进行了建模,并通过巧妙的电生理实验测到了各门控变量随膜电位变化的转换速率,最终搭建了一个强大的神经元模型。HH模型的建模几乎全部基于生物学事实,每个动力学方程都有对应的生物学机制,因此,该模型具有很强的动力学表征能力,既能精准模拟神经元的动作电位,又能解释其背后的生物学原因,是将生物实验与数学方法融合的经典模型。
在第3章,我们将介绍一些简化神经元模型。它们的建模思路与HH模型有较大差别,一些动力学方程并没有严格的生物学基础,但仍然能够表征神经元的动力学行为。
2.9 拓展阅读:求解门控变量n、h、m 的表达式
2.9.1 门控变量n
2.9.2 门控变量h
2.9.3 门控变量m
第 3 章 简化神经元模型
3.1 泄漏整合发放(LIF)模型
3.1.1 LIF 模型的定义
3.1.2 LIF 模型的动力学性质
3.1.3 LIF 模型的优点和缺点
3.2 二次整合发放(QIF)模型
3.2.1 QIF 模型的定义
3.2.2 QIF 模型的动力学性质
3.2.3 θ 神经元模型
3.3 指数整合发放(ExpIF)模型
3.3.1 ExpIF 模型的定义
3.3.2 ExpIF 模型的动力学性质
3.4 适应性指数整合发放(AdEx)模型
3.4.1 AdEx 模型的定义
3.4.2 AdEx 模型的发放模式
3.4.3 利用相平面分析法研究AdEx 模型产生不同发放模式的动力学机制
3.5 Izhikevich 模型
3.5.1 Izhikevich 模型的定义
3.5.2 Izhikevich 模型的发放模式
3.5.3 用分岔分析法研究Izhikevich 模型在不同发放模式间的转换
3.6 Hindmarsh-Rose(HR)模型
3.6.1 Hindmarsh-Rose 模型的定义
3.6.2 Hindmarsh-Rose 模型产生簇发放的动力学机制
3.6.3 Hindmarsh-Rose 模型的其他发放模式
3.7 泛化整合发放(GIF)模型
3.7.1 GIF 模型的定义
3.7.2 GIF 模型的动力学分析
3.8 本章小结
本章介绍了几种常见的简化神经元模型及其动力学性质。LIF模型是最简单的简化神经元模型,有一个单变量的线性微分方程和一个条件判断组成;QIF模型和ExpIF模型也是单变量模型,但在微分方程中增加了非线性项,使得膜电位的变化更接近真实神经元的情况;AdEx模型和Izhikevich模型分别是ExpIF模型和QIF模型的延伸,它们属于双变量模型,除膜电位外,还增加了一个变量,以刻画神经元的适应性或膜电位恢复程度,大大增强了神经元的动力学表征能力;Hindmarsh-Rose模型是一个三变量模型,通过两个快变量和一个慢变量的微分方程来控制神经元的发放,不再需要显式地重置膜电位和其他变量;GIF模型包含多个变量,但其微分方程都是线性的,其广泛的表征能力主要来自多变量和复杂的更新规则。
除了常见的简化神经元模型,我们还学习了一些常用的动力学分析方法并将其用于实践。在分析QIF模型和ExpIF模型的动力学性质时,我们使用了一维相平面分析法。在研究AdEx模型时,我们使用了二维相平面分析法,通过该方法能够便利和直观地理解神经元动力学特性和各种发放模式。在研究Izhikevich模型时,我们利用分岔分析法研究了参数变化对模型动力学性质的影响,并讨论了分岔分析法和相平面分析法,还有一些分析方法可以用于高维动力学系统的分析,我们将在后面的章节中介绍。
第 3 篇 突触及突触可塑性模型
第 4 章 突触模型
4.1 化学突触
4.2 化学突触的现象学模型
4.2.1 电压跳变模型
4.2.2 指数衰减模型
4.2.3 Alpha 函数模型
4.2.4 双指数衰减模型
4.3 化学突触的生理学模型
4.3.1 建模离子通道的开放与关闭
4.3.2 AMPA 模型和GABAA 模型
4.3.3 NMDA 模型
4.3.4 GABAB 模型
4.4 电突触模型
4.5 本章小结
本章主要介绍了静态突触的建模。突触可以分为化学突触和电突触,它们的功能不尽相同。在化学突触的建模中,只关心突触电导的变化曲线而不关心其生物学机制的模型被称为现象学模型。我们介绍了电压跳变模型、指数衰减模型、Alpha函数模型和双指数衰减模型等现象学模型。与之相对,生理学模型从化学突触生理结构的角度对其动力学性质进行建模。我们对神经系统中常见的AMPA 受体、GABAA受体、NMDA受体和GABAB受体进行了建模。除了化学突触,还有一种由间隙连接构成的电突触。其模型相对简洁且单一,不过我们能够通过模拟看到相邻神经元通过电突触对彼此造成的影响。
第 5 章 突触可塑性模型
5.1 突触短时程可塑性
5.2 突触长时程可塑性
5.2.1 脉冲时序依赖可塑性(STDP)
5.2.2 赫布学习法则
5.2.3 Oja 法则
5.2.4 BCM 法则
5.3 本章小结
本章介绍了突触可塑性模型。突触可塑性指突触效能(神经元的连接强度)的变化。根据其所能维持的时长,可以将突触可塑性分为短时程可塑性(Short-Term Plasticity,STP)和长时程可塑性(Long-Term Plasticity,LTP),它们的产生机制有所不同。STP的持续时间为毫秒级到秒级,主要由突触前神经元内部的暂时性变化引起,如激发神经递质释放的钙离子浓度、神经递质的剩余量等,其建模从该角度入手。长时程可塑性的持续时间可以是几十秒以上,甚至不可逆,目前的模型一般尝试模拟长时程可塑性的现象,而不是从产生的机制入手,包括STDP、赫布学习法则、Oja法则、BCM法则等。突触可塑性被认为是大脑实现学习、记忆、实时计算等功能的核心。
第 4 篇 神经网络模型
第 6 章 兴奋—抑制平衡网络
6.1 兴奋—抑制平衡网络的结构
神经科学研究的目的之一是寻找大脑编码信息的可能法则。……研究者通过大量神经生物学实验发现,在同样的外部刺激下,大脑皮层中的神经元每次产生的脉冲序列都不同,且单次脉冲序列表现出极不规律的统计行为,其fano因子甚至大于随机泊松过程,这位我们理解神经编码带来了很大困扰。同时,有实验发现,如果切断神经元之间的连接,单独对皮层切片施加恒定刺激,神经元会产生规律发放,这说明完整大脑中神经元的不规律发放源于神经网络的内部性质,而不是单神经元特性。
6.2 兴奋—抑制平衡网络的编程实现
6.3 兴奋—抑制平衡网络的计算功能
6.4 本章小结
本章介绍了兴奋—抑制平衡网络,在该网络中,兴奋性神经元和抑制性神经元随机稀疏连接,且兴奋性输入和抑制性输入的强度大致平衡,基本抵消,使得网络被外部输入激发时表现出足够的不规律性。尽管网络在内部结构上存在大量的随机因素,但在整体上却具有规律的表现,如网络对外部刺激呈现线性反应(这种线性不依赖神经元模型本身对外部输入的反应),且可以快速跟踪外部刺激的变化等。通过该模型,我们可以获得大脑编码外部信息的一个法则:有时单神经元对外部刺激的编码呈现不规律性,但由成千上万个神经元构成的神经元群却能够产生有规律的响应。因此,我们在学习计算神经科学时不仅要关注单神经元模型的构建,还要研究由它们构成的神经网络的结构及计算性质,从神经元群的角度理解大脑编码和处理信息的方式。与之对应,在编程上我们也要学会利用神经元和突触连接快速搭建网络,以实现高效的模拟和运算。
第 7 章 决策网络
7.1 决策行为的研究背景
决策是重要的认知行为,它意味着大脑不仅能感知外部信息,还能根据这些信息做出选择。这种处理在外部信息所对应的选择倾向一致时会比较直观,但如果相互矛盾的信息同时出现,决策过程就会十分复杂,需要花费很长时间。……
7.2 脉冲决策网络
7.2.1 脉冲决策网络的结构
7.2.2 脉冲决策网络模型的编程实现
7.3 发放频率决策网络
7.3.1 发放频率决策网络的结构
7.3.2 发放频率决策网络模型的编程实现
7.3.3 发放频率决策网络模型的动力学分析
7.4 本章小结
本章探究了决策网络的结构、实现方式和计算性质。为模拟大脑利用给定信息做出决策的方式,我们用两种模型实现了决策网络。脉冲神经网络模型以脉冲神经元模型为单位构建网络,其具有较强的生物可解释性,很好地复现了猕猴在运动辨别任务中的决策表现。该网络的特点之一是神经元群不是根据某个时刻的刺激做出决策,而是在时间尺度上积累了一定的输入后,在获得了充足“证据”的情况下做出决策。这样的决策模式对噪声的抵抗性更好、鲁棒性更强。为了在理论层面更好地解释决策网络的行为表现,我们简化了模型,分别用发放频率单元代替两个神经元群,从而构建了发放频率决策网络模型。因为有了两个发放频率单元的数学表示,我们可以利用二维相平面分析法考察网络对外部输入的响应,由此发现了网络的双稳态性质,而网络最终达到哪个稳态则依赖外部输入的变化。在决策网络的研究中,我们不仅再次看到神经元群作为一个整体共同编码和处理信息的普遍形式,还体会了数学工具在生物模型中的应用,使我们在理论层面对模型有了更深的理解。
第 8 章 连续吸引子网络
8.1 吸引子网络
本章介绍一类重要的神经网络模型——吸引子网络(Attractor Network)。吸引子网络由多个结点(神经元)相互连接组成的动力学网络,在不接受外部输入的情况下,网络的状态会逐渐达到一个稳定的状态。这个稳定的状态被称为吸引子(Attractor)。一般来说,一个吸引子网络往往存在多个稳定状态,其数量由网络结构和结点数量决定。吸引子网络被用于解释许多认知现象,特别是与信息表达相关的认知功能。
代表:Amari-Hopfield网络
8.2 连续吸引子网络的结构
8.3 连续吸引子网络模型的编程实现.
8.4 连续吸引子网络模型的计算功能
8.4.1 神经元群编码
8.4.2 平滑跟踪
8.4.3 其他计算功能
8.5 本章小结
本章我们认识了吸引子网络,重点研究了连续吸引子网络的结构和性质。连续吸引子网络的特点是网络中存在多个稳定点,且这些稳定点在网络状态空间中连续分布,网络能够轻松地从一个稳定状态平滑转移到相邻的稳定状态。连续吸引子网络存在多种数学表示,但无论哪种都抓住了“连续吸引子”的核心特点。我们通过对一种理论可解模型的探讨,发现连续吸引子网络的计算性质包括:为群体编码提供自然的实现形式,网络的抗噪声能力强,能够平滑跟踪外部刺激的运动。此外,连续吸引子网络还具有生物学意义和许多计算功能,越来越多的理论和生物研究表面,连续吸引子网络很可能是大脑加工和编码外部信息的基本形式之一。
第 9 章 库网络
9.1 库网络的定义及发展背景
库网络(Reservoir Network)是循环神经网络(Recurrent Neural Network,RNN)的一种,通常有一个(或多个)随机连接的神经元群和一个读取层(Readout Layer)构成,其中随机连接的神经元群被称为库(Reservoir)。……
2001年和2002年,Jaeger和Maass先后提出了具有库网络特征的模型,被称为回声状态网络(Echo State Network,ESN)模型和液体状态机(Liquid State Machine,LSM)模型。这两个模型的结构十分相似,只不过ESN模型用人工神经网络的形式实现,LSM模型用脉冲发放网络的形式实现。当时“库网络”的概念还没有形成,这些研究是在不同地点、不同时间独立完成的。后来,人们意识到了它们的共通之处,才将这类由随机连接的循环网络表征信息、由输出层承担训练任务的网络统称为库网络,一个全新的研究分支就此形成。
库网络领域中的经典模型就是ESN模型和LSM模型。因为这两个模型的建模思路和动力学性质相似,只是实现形式有区别,所以我们只对ESN模型进行讲解,对LSM模型感兴趣的读者可以阅读相关文献。
9.2 回声状态网络的定义和限定条件
9.2.1 回声状态网络的定义
9.2.2 网络具有回声性质的条件
9.3 回声状态网络模型的编程实现
9.4 回声状态网络的训练
9.4.1 周期(正弦)函数的拟合
9.4.2 劳伦兹系统的预测
9.5本章小结
本章以ESN为例介绍库网络的结构和计算性质。从结构上看,库网络是一个简单的循环神经网络,其内部的循环连接是随机的,甚至不被训练,那么库网络的计算性质究竟从何而来?其实,库网络对输入信息的复杂处理正是来自其随机循环连接。由于循环连接的存在,网络能够整合输入的序列信息,并将其保存在神经元的状态中:每个神经元既能通过正向连接接收当前时刻的外部输入,又能通过循环连接接收各神经元上一时刻的状态,这个迭代过程使得神经元能够保留较多的历史输入信息,从而达到了整合历史信息的目的。随机的连接使不同神经元的状态有不同的意义,而回声性质保证了所有神经元的状态仅依赖外部的序列输入,从而保证了系统的稳定(值得一提的是,这里所指的“序列输入”不一定是时间序列,可以是任何具有序列特性的信息)。其实,库网络暗含了一种类似核函数的思想:核函数将外部输入先映射到一个(往往是高维的)特征空间,这样对特征空间的数据处理就会更容易,而库网络中的库正是通过循环连接和激活函数对序列信息进行了整合和非线性化操作,以获取潜在有用的高维特征。在将库网络应用于三角函数拟合和劳伦兹系统的预测时,我们也看到了训练后的库网络很好地抓住了系统的非线性特征,获得了良好的拟合和预测结果。
第 10 章 网络模型总结
本篇介绍了计算神经科学领域的4个经典网络:兴奋——抑制平衡网络、决策网络、连续吸引子网络和库网络。这些网络能够作为经典长期流行的原因,除了在于其提出时基于有意义的科学问题,还在于它们背后的思想具有超前的普适性。例如兴奋——抑制平衡网络是为了解释电生理实验中观察到的神经元不规律发放现象而提出的,但其提出的兴奋性输入和抑制性输入的平衡性正是网络能够在外部输入下快速响应的关键,后续研究也表明这样的网络结构可能普遍存在于各脑区;决策网络能够优雅地模拟决策过程中证据积累的过程,原因在于网络本身具有两个吸引子,分别对应两个决策结果,这体现了模型的外在行为和内在动力学性质密不可分的联系;连续吸引子网络在提出时就具有较为宏大的思想,即成为大脑信息表征的正则化模型,后来的研究也证明该网络模型能够广泛应用于连续变量的编码,从而解释许多认知和计算问题;库网络暗含一种类似“核函数”的思想,通过循环连接整合历史序列信息并将其表征到高维空间,使得之后的数据处理能够通过线性操作轻松完成,也能节省计算资源。因此,我们在学习这些模型的时候,不仅需要知道它们的结构和具体实现,还应该了解它们的发展历史和背后蕴含的科学思想,以做到举一反三、融会贯通。
参考文献
附录——书评
谁不对破译大脑的奥秘(如意识、情感、智力本质等)感兴趣呢?
近年来,脑科学在世界范围内越来越受重视,多个国家已经启动了雄心勃勃的大型脑科学计划,关于大脑结构和神经活动的海量实验数据不断涌现。
我们要完整地认识大脑,实验与计算这两个方面的知识缺一不可,我们不仅要知道大脑的结构(实验神经科学)与认知功能(认知神经科学、心理学),还要阐明这些神经结构是如何实现大脑的认知功能的(计算神经科学)。
本书的主要内容
01 计算神经科学是什么
计算神经科学的目标是用计算建模的方法阐明大脑的工作原理。
“阐明”的标准是用数学模型详细描述从结构到功能的计算过程,这样才能在真正意义上理解大脑的工作机制。这些模型可以应用于人工智能或启发人工智能的发展,即实现所谓的类脑智能。因此,计算神经科学是脑科学与人工智能之间的桥梁。
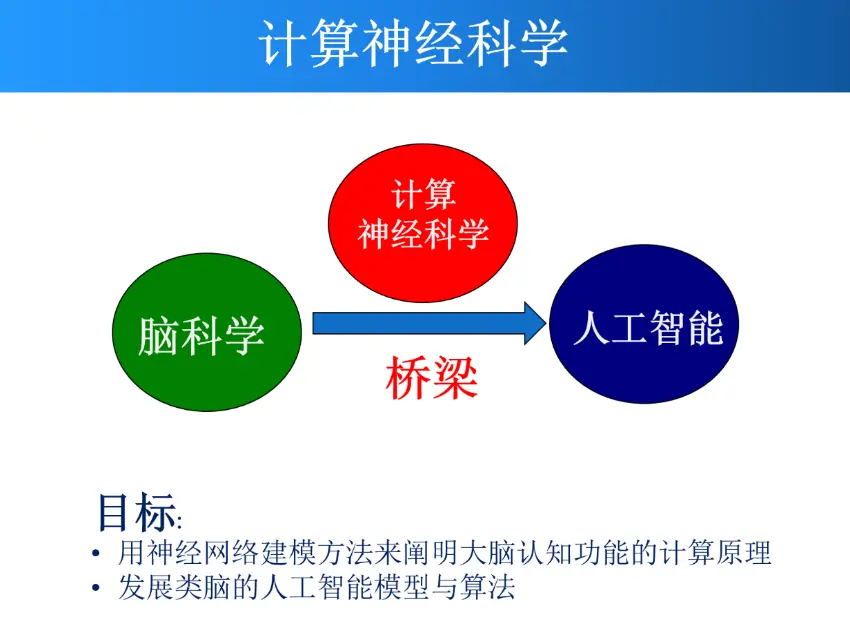
计算神经科学不仅可以帮助我们理解大脑进行信息加工的基本原理,有助于治疗癫痫、自闭症、老年痴呆等神经退行性疾病,还可以为人工智能的发展提供灵感和指导,推动新一代神经形态芯片的设计。
如果你想快速、深入、全面地了解这门学科,那么一定不要错过这本由北京大学神经信息处理实验室撰写的新书:《神经计算建模实战:基于BrainPy》。

02 本书涵盖了众多基础模型
本书全面系统地介绍了神经系统中各个层次的基础计算模型,从单个神经元到复杂的神经网络,从生物物理到认知功能。
首先,本书从神经元开始,讲述了如何用数学方程描述真实的神经元,并介绍了一系列简单易用的抽象神经元模型。
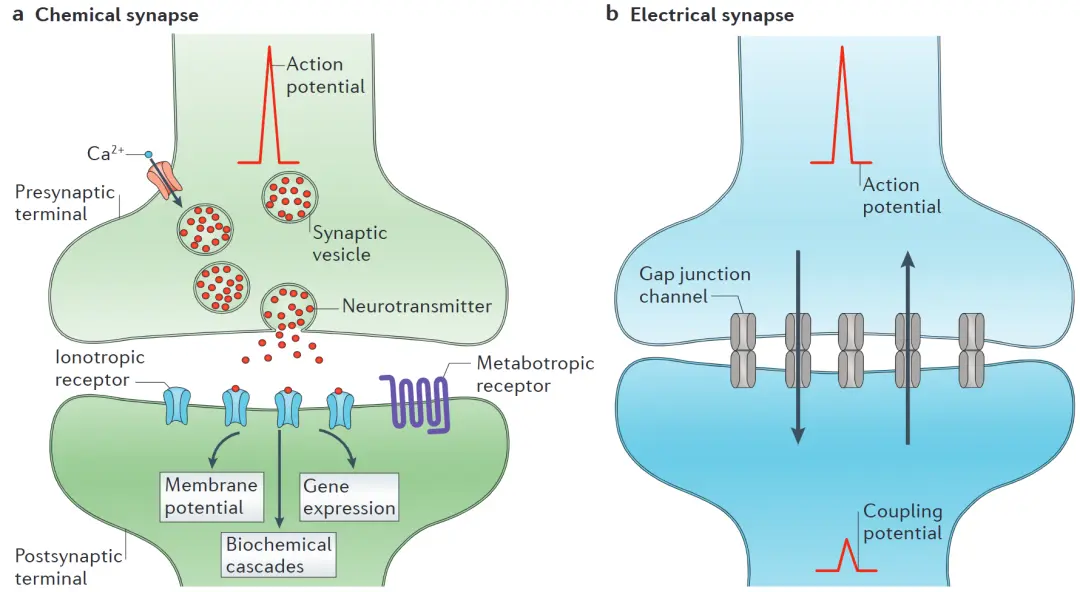
其次,本书讲述了神经元之间如何通过化学突触和电突触来传递信号,并介绍了不同类型的突触模型。
再次,本书还介绍了突触可塑性模型,这是神经系统发育、学习、记忆与认知的重要机制。具体包括短时程可塑性和长时程可塑性两种主要形式。
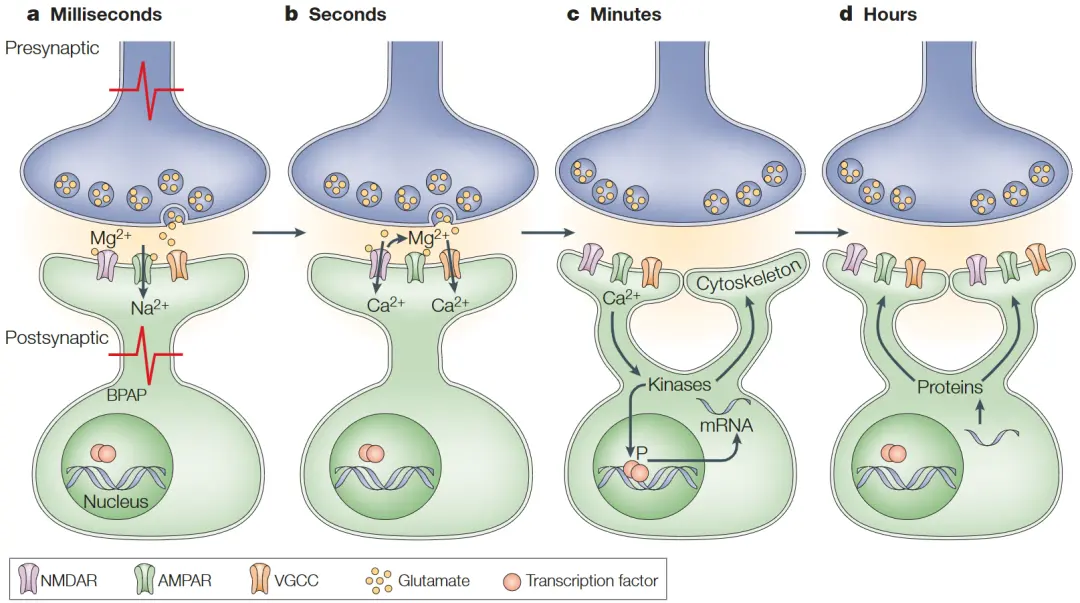
最后,本书还介绍了一些典型的大脑网络模型,展示了神经元和突触如何协同工作,以实现不同的功能。例如,兴奋—抑制平衡网络、决策网络、连续吸引子网络、库网络等。
03 BrainPy编程实现
本书不仅详细介绍了不同层次的理论模型,还为每个模型配套了相应的代码实现。所有代码使用原创的BrainPy编程框架实现。
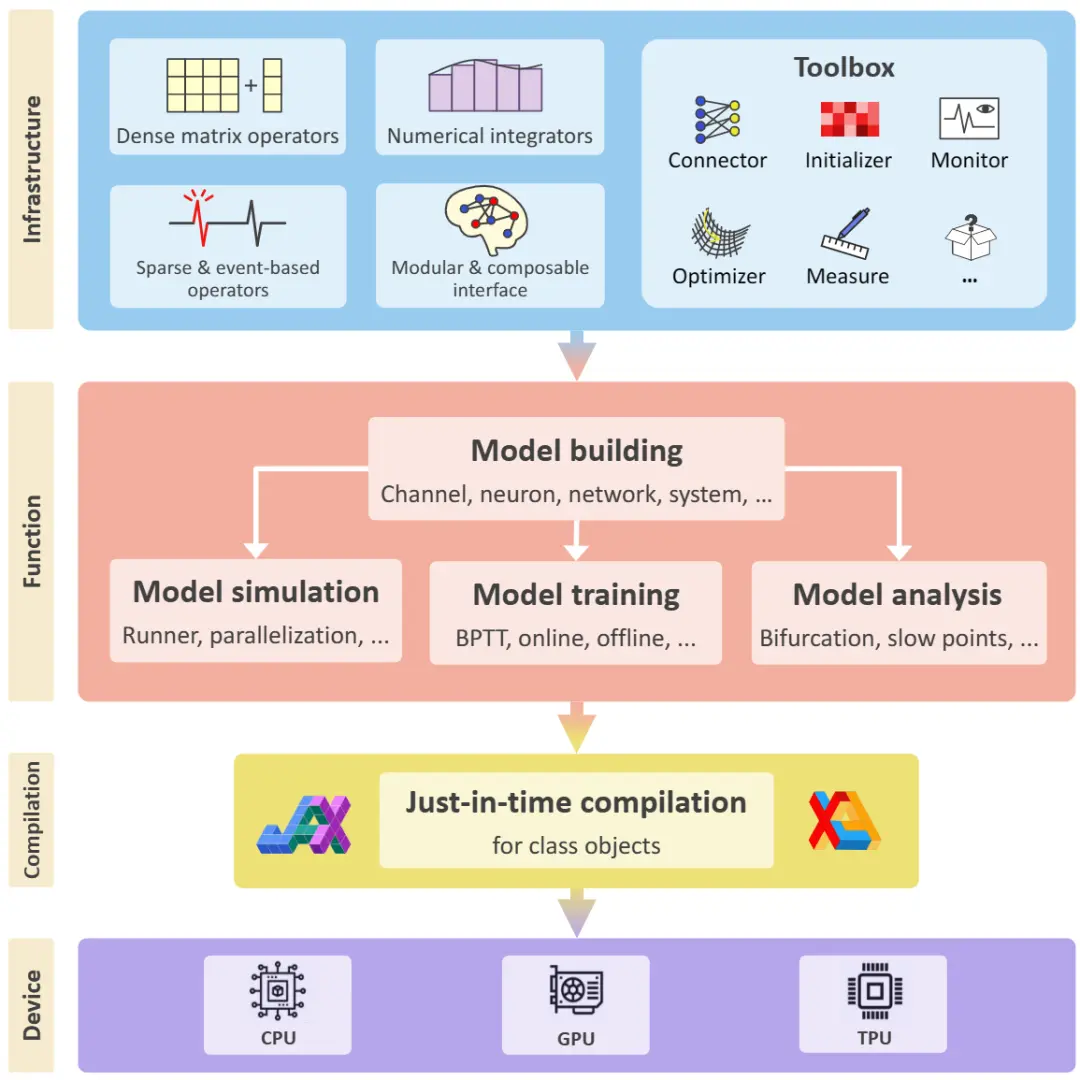
BrainPy是一套专为脑动力学模型设计的通用编程软件,它可以方便地定义、模拟、训练和分析各种计算神经科学模型与类脑计算模型。通过阅读本书,你不仅可以学习到丰富的神经计算建模知识,还可以掌握如何使用该软件。
本书的作者团队
本书由北京大学神经信息处理实验室的吴思教授团队撰写。吴思教授是北京大学心理与认知科学学院教授,IDG麦戈文脑科学研究所、定量生物学中心、北京大学—清华大学生命科学联合中心研究员,北京智源学者。研究领域是计算认知神经科学和类脑计算。
吴思教授在计算神经科学领域开展科研和教学工作20余年,为推动中国计算神经科学的发展贡献了力量,参与组织了多个短期培训课程,如已有10余年历史的冷泉港—亚洲暑期课程、上海交通大学冬季课程等。
在日常科研中,时常有学生或来自其他领域的学者表示对计算神经科学有强烈兴趣,希望能推荐一本简单易懂的、理论与实践紧密结合的入门教材,于是就有了本书。
